GEM² - GRUPO DE ESTUDO EM MODELOS MISTOS

Geral

1. Estudar modelos misto em uma abordagem teórica e computacional

Especificos, Abordodagem em:

1. Experimentação Agropecuária
2. Genética
3. Modelagem Ambiental

• Paulo Justiniano Ribeiro Jr
• Silvia Emiko Shimakura
• Wagner Hugo Bonat
• Walmes Marques Zeviani
• Fernanda Bührer Rizzato
• Cesar Taconeli
• Eder David Borges da Silva
• Renato Gonçalves de Oliveira

• Random Effects - Faraway
• Scritps Extending the Linear Model with R
• Random Effects Material Atualizado do livro
• João Gil de Luna

• John Fox - Introduction to Mixed-Effects Models for Hierarchical and Longitudinal Data (I);
• John Fox - Introduction to Mixed-Effects Models for Hierarchical and Longitudinal Data (II);
• Claudia Czado - Lecture Notes on Linear Mixed Models;
• R. D. Murison - Mixed Models Lecture Notes;
• Søren Højsgaard & Erik Jørgensen - Lecture Slides on Mixed Models;
• Jason Fridley - Lecture notes from Bio793: Plant Ecology/Niche modeling/Modeling in R;
• Mixed-Effect Models and Longitudinal Data Analysis -- Lecture Notes;
• Elizabeth Ann Housworth - Lecture Notes for M761: Topics in Applied Statistics;
• Roger Levy - Linguistics 251: Probabilistic Methods in Linguistics;
• Dan Nettleton - Statistics 511 Lecture Notes;
• Peter D. Hoff - CSSS-Statistics 560 Lecture Notes;
• Lauri Mehtätalo - Forest biometrics with examples in R;
• Tim Hanson - Stat 771: Longitudinal Data Analysis;
• Lectures notes on generalized mixed models;
• yeroon.net/lme4 R Web Application;
• Douglas Bates - Mixed models in R using the lme4 package;
• Douglas Bates - Fitting Linear Mixed-Effects Models Using the lme4 Package in R;
• Douglas Bates - Generalized Linear and Nonlinear Mixed-Effects Models;
• Douglas Bates Tour em Amsterdam(2011), Madson(2011), Gaithersburg(2010), Seewiesen(2009), Rennes(2009), Lausanne(2009);
• John Maindonald - The Anatomy of a Mixed Model Analysis, with R's lme4 Package;
• [R] GLMM (lme4) vs. glmmPQL output (summary with lme4 revised);
• Los Angeles area R users group (data analysis/statistics);
• Hugo Quené - Mixed-effects modeling with crossed random effects in R;
• Hugo Quené - Mixed-Effects Modeling Multilevel Modeling;
• Using lmer and nlme at the same time;
• Brief Introduction to LINEAR MIXED MODELS in R;
• Research and Statistical Support;
• Linear Mixed Models Appendix to An R and S-PLUS Companion to Applied Regression - John Fox;
• Likelihood Ratio Tests in Linear Mixed Models with One Variance Component - Ciprian M. Crainiceanu and David Ruppert;
• Maximum Likelihood Algorithms for Generalized Linear Mixed Models - Charles E. McCulloch;
• Generalized Maximum Likelihood Method in Linear Mixed Models with an Application in Small-Area Estimation - P.Lahiri and Huilin Li;
• CONDITIONAL LIKELIHOOD INFERENCE IN GENERALIZED LINEAR MIXED MODELS N. Sartori and T. A. Severini;
• Mixed models in R using the lme4 package Part 6: Nonlinear mixed models Douglas Bates;
• Likelihood Inference for Models with Unobservables: Another View - Youngjo Lee and John A. Nelder;
• Asymptotic Properties of Maximum Likelihood Estimates in the Mixed Model of the Analysis of Variance;
• A direct derivation of the REML likelihood function;
• Topics in Mixed Effects Models - José Carlos Pinheiro;
• A CLASSICAL APPROACH FOR THE ANALYSIS OF GENERALIZED LINEAR MIXED MODELS - MJ Hammujuddy;
• Marginal maximum likelihood estimation of variance components in Poisson mixed models using Laplacian integration;
• Longitudinal data, mixed models and incomplete data - Geert;
• Thomas Kneib - Restricted maximum likelihood estimation of variance components in generalized linear mixed models;
• Fit generalized linear mixed models (GLMM), using of different likelihoods;

• Em preto: conteúdo abordado no encontro;
• Em verde: conteúdo previsto para o próximo encontro;

—-

• (17/06/2011)
  • WB: disponibilizar os scripts apresentadas em 17/06;
  • WZ: preparar documento com a distribuição marginal em LMM;
  • PJ & WZ: preparar documento com a derivação e implementação (didática) do método REML;
• (01/07/2011)
  • WZ: documentar os procedimentos de estimação empregando métodos numéricos para a integração dos efeitos aleatórios escritos por WB, rodar glmm.PQL(), glmer();
  • SS: implementar o PQL;
  • EB: implementar o REML;
  • PJ: procedimentos para predição dos efeitos aleatórios;

[200?, book]

Magalhães, M. N., & Lima, A. C. P. (200?). Noções de Probabilidade e Estatística (1 ed.) Edusp.

[2009, techreport | www]

Ribeiro Júnior, P. J. (2009). Introdução ao Ambiente Estatístico R.

[2002, book | www]

Venables, W. N., & Ripley, B. D. (2002). Modern applied statistics with S Birkhäuser.

[2009, book | www]

Everitt, B. S., & Hothorn, T. (2009). A Handbook of Statistical Analyses Using R, Second Edition (2 ed.) Chapman \& Hall.

[2008, book | www]

Dalgaard, P. (2008). Introductory Statistics with R (2nd ed.) Springer.

[2008, book | www]

Sarkar, D. (2008). Lattice: Multivariate Data Visualization with R (1 ed.) Springer.

1. The R project for Statistical Computing: página do programa R
   1. nlme Linear and Nonlinear Mixed Effects Models
2. Uma página interessante com um introdução ao R
3. O Xemacs é uma outra opção de editor que facilita a edição de arquivos do 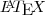e R e disponível para plataformas Linux e Windows.
4. R-br é a lista de discussão em português sobre o uso do R

### Modelo mistos
### Exemplo retirado do capitulo Random Effeets do Faraway
require(faraway)
require(lme4)
###------------------------------------------------------------###
### Modelo simples com apenas um fator
data(pulp)
str(pulp)
summary(pulp)
op <- options(contrasts=c("contr.sum", "contr.poly"))
### Efeitos Fixos
lmod <- aov(bright ~ operator, pulp)
summary(lmod)
summary.lm(lmod)
coef(lmod)
 
sigma2alfa <- (0.447-0.106)/5
sigma2alfa
 
model.matrix(lmod)
 
modelo <- matrix(apply(model.matrix(lmod),1,function(x){coef(lmod)*x}),ncol=4,byrow=TRUE)
compoF <- cbind(pulp$bright,modelo,lmod$res)
colnames(compoF) <- c('var','Intercept','operator1','operator2','operator3','erro')
compoF
 
rowSums(compoF[,-1])
compoF[,1]
summary(lmod)
 
SQV <- sum(compoF[,1]^2)
SQI <- sum(compoF[,2]^2)
SQT <-sum(rowSums(compoF[,3:5])^2)
SQE <- sum(compoF[,6]^2)
 
SQTc <- SQV-SQI
SQTc
SQT
SQE
summary(lmod)
 
SQTc 
SQT+SQE
 
### Efeitos aleatorios
mmod <- lmer(bright ~ 1+(1|operator), pulp)
summary(mmod)
str(mmod)
 
compoM <- matrix(0,nrow=20,ncol=3)
compoM[,1] <- fixef(mmod)
compoM[,2] <- rep(ranef(mmod)$operator[,1],each=5)
compoM[,3] <- residuals(mmod)
compoM <- cbind(pulp$bright,compoM)
colnames(compoM) <- c('var','intercepto','efeito','erro')
compoM
 
smod <- lmer(bright ~ 1+(1|operator), pulp,method="ML")
summary(smod)
 
compoS <- matrix(0,nrow=20,ncol=3)
compoS[,1] <- fixef(smod)
compoS[,2] <- rep(ranef(smod)$operator[,1],each=5)
compoS[,3] <- residuals(smod)
compoS <- cbind(pulp$bright,compoS)
colnames(compoS) <- c('var','intercepto','efeito','erro')
compoS
 
SQE <- t(compoS[,'erro'])%*%compoS[,'erro']
SQE
rowSums(compoS[,-1])
pulp$bright
 
## Inferencia
# Modelo nulo
nullmod <- lm (bright ~ 1, pulp)
summary(nullmod)
 
##LRT
tLRT <- as.numeric(2*(logLik(smod)-logLik(nullmod)))
tLRT
pchisq(tLRT,1,lower=FALSE)
 
## Comparando os dois modelos
anova(mmod,smod)
 
#bootstrap
y <- simulate(nullmod,50)
#y
 
### Visualizando a simulação
hist(pulp$bright,prob=T)
apply(y,2,function(x){lines(density(x))})
lines(density(pulp$bright),lw=2,col='red')
 
## Bootstrap
lrstat <- numeric(1000)
for(i in 1:1000){
  y <- unlist(simulate(nullmod))
  bnull <- lm(y ~ 1)
  balt <- lmer(y~1 + (1|operator),pulp,method="ML")
  lrstat[i] <- as.numeric(2*(logLik(balt)-logLik(bnull)))
}
 
hist(lrstat)
summary(lrstat)
 
mean(lrstat < 0.0001)
 
# pvalor bootstrap
pb <- mean(lrstat > 2.5684)
pb
 
## Erro padrão boosstrap
standErro <- sqrt(pb*(1-pb)/1000)
standErro
 
# Prediçao
ranef(mmod)$operator
 
cc <- model.tables(lmod)
cc
 
###Shirikange
shir <- cc[[1]]$operator/ranef(mmod)$operator
shir
 
blups <- fixef(mmod)+ranef(mmod)$operator
blups
 
## Residuos
par(mfrow=c(1,2))
qqnorm(resid(mmod),main="")
plot(fitted(mmod),resid(mmod),xlab="Fitted",ylab="Residuals")
abline(0,0)
 
###------------------------------------------------------------###
### Modelo com efeito de bloco
rm(list=ls())
data(penicillin)
summary(penicillin)
 
## Modelo fixo
op <- options(contrasts=c("contr.sum", "contr.poly"))
lmod <- aov(yield ~ blend + treat, penicillin)
summary(lmod)
coef(lmod)
 
compoF <- matrix(0,nrow=20,ncol=4)
compoF[,1] <- coef(lmod)[1]
compoF[,2] <- rep(c(coef(lmod)[2:5],0-sum(coef(lmod)[2:5])),each=4)
compoF[,3] <- rep(c(coef(lmod)[6:8],0-sum(coef(lmod)[6:8])),5)
compoF[,4] <- lmod$res
compoF <- cbind(penicillin$yield,compoF)
colnames(compoF) <- c('var','intercepto','bloco','efeito','erro')
compoF
rowSums(compoF[,-1])
compoF[,1]
 
## Modelo misto
mmod <- lmer (yield ~ treat + (1|blend), penicillin)
summary(mmod)
 
ranef(mmod)$blend
fixef(mmod)
 
compoM <- matrix(0,nrow=20,ncol=4)
compoM[,1] <- fixef(mmod)[1]
compoM[,2] <- rep(ranef(mmod)$blend[,1],each=4)
compoM[,3] <- rep(c(fixef(mmod)[2:4],0-sum(fixef(mmod)[2:4])),5)
compoM[,4] <- residuals(mmod)
compoM <- cbind(penicillin$yield,compoM)
colnames(compoM) <- c('var','intercepto','bloco','efeito','erro')
compoM
rowSums(compoM[,-1])
compoM[,1]
 
anova(mmod)
 
amod <- lmer (yield ~ treat + (1|blend), penicillin,method="ML")
nmod <- lmer (yield ~ 1 + (1|blend), penicillin,method="ML")
anova(amod,nmod)
 
## bootstrap
lrstat <- numeric(1000)
for(i in 1:1000){
  ryield <- unlist(simulate(nmod))
  nmodr <- lmer(ryield ~ 1 + (1|blend), penicillin,method="ML")
  amodr <- lmer(ryield ~ treat + (1|blend), penicillin,method="ML")
  lrstat[i] <- 2*(logLik(amodr)-logLik(nmodr))
}
 
plot(qchisq((1:1000)/1001,3),sort(lrstat),xlab=expression(chi[3]^2),ylab="Simulated LRT")
abline(0,1)
 
mean(lrstat > 4.05)
 
rmod <- lmer(yield ~ treat + (1|blend), penicillin)
nlmod <- lm(yield ~ treat, penicillin)
2* (logLik(rmod)-logLik(nlmod,REML=TRUE))
 
lrstatf <- numeric(1000)
for(i in 1:1000){
  ryield <- unlist(simulate(nlmod))
  nlmodr <- lm(ryield ~ treat, penicillin)
  rmodr <- lmer(ryield ~ treat + (1|blend), penicillin)
  lrstatf [i] <- 2*(logLik(rmodr)???logLik(nlmodr,REML=TRUE))
  }
 
mean(lrstatf < 0.00001)
 
cs <- lrstatf[lrstatf > 0.00001]
ncs <- length(cs)
 
plot(qchisq((1:ncs)/(ncs+1),1),sort(cs),xlab=expression(chi[1]^2),ylab="Simulated LRT")
abline (0,1)
 
mean(lrstatf > 2.7629)
 
###------------------------------------------------------------###
### Modelo em parcelas Subdivididas
data(irrigation)
str(irrigation)
summary(irrigation)
attach(irrigation)
 
### Modelo com mais parametros que variáveis
#lmod <- lmer (yield ~ irrigation * variety + (1|field) + (1|field:variety),data=irrigation)
 
lmodr <- lmer (yield ~ irrigation * variety + (1|field),data=irrigation)
logLik(lmodr)
summary(lmodr)
 
anova(lmodr)
 
mod <- aov(yield ~ irrigation * variety + Error(field),data=irrigation)
summary(mod)
 
mod <- lm(yield ~ irrigation * variety+field/variety,data=irrigation)
anova(mod)
 
model.matrix(mod)