Página WIKI de José Cláudio Faria

Na Praia do Sul de Ilhéus, em janeiro de 2007, refletindo profundamente sobre o R!!!

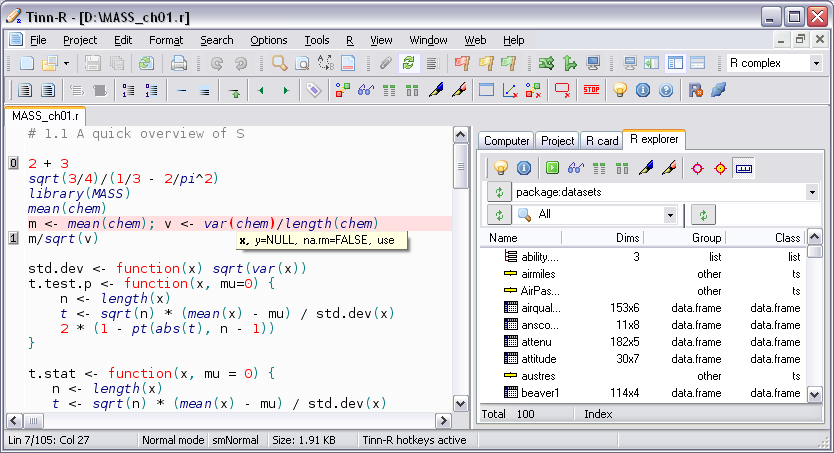
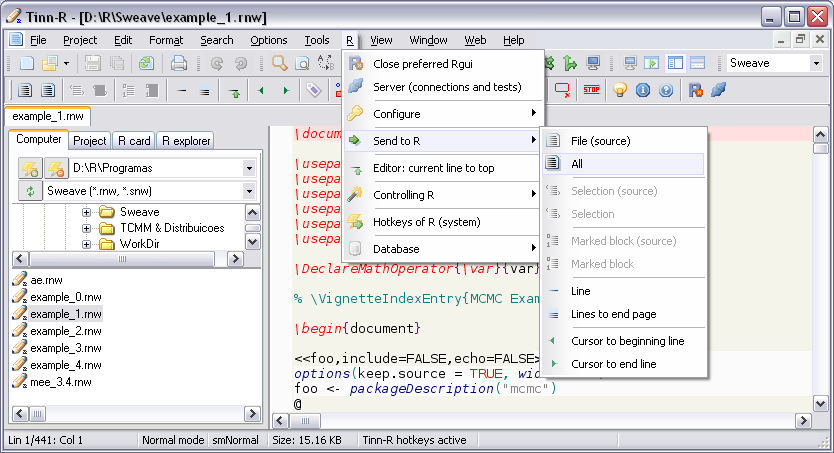
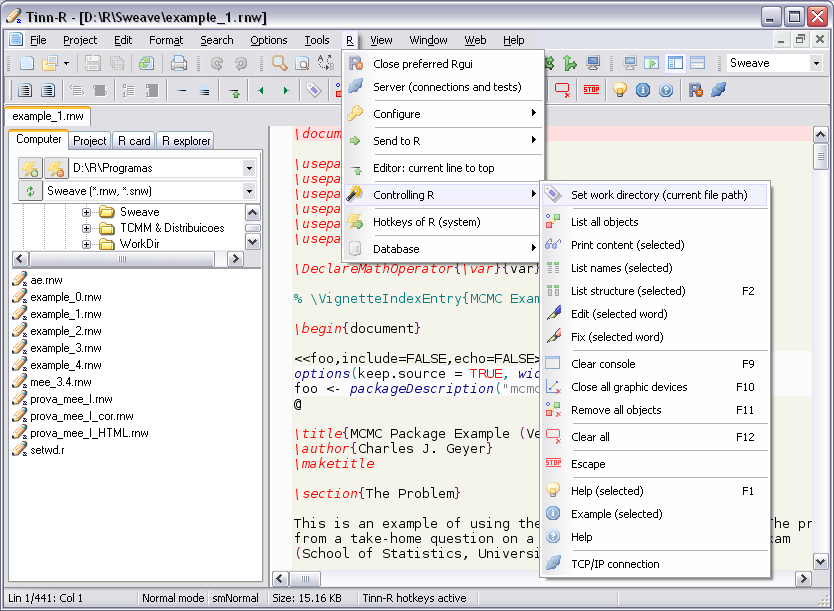
Tinn-R GUI/Editor para o ambiente R sob Windows.

• O Tinn-R é um programa de código aberto (sob GPL) desenvolvido em Object Pascal com a IDE Delphi_7 da Borland;
• Facilita o uso do interpretador R e aumenta a produtividade das análises e documentações;
• Possui, além dos recursos inerentes aos bons editores, ferramentas avançadas de conversão de formato de arquivos e compilação: Txt2tags, Deplate, Miktex;
• Suporte ao Sweave;
• Permite interagir com o R em modo gráfico, o que aumenta a produtividade e facilita o uso, ao mesmo tempo em que estimula o aprendizado da linguagem R;
• Imagens:
  • 
  • 
  • 

Abrir no Tinn-R e executar linha por linha buscando entender cada passo:

#===============================================================================
# Título: Introdução ao R - IR
# Curso : Métodos estatísticos aplicados à produção vegetal
# Autor : José Cláudio Faria/UESC/DCET
# Data  : 15/12/06 18:39:16
# Versão: v7 - com comentários - cc
# Objetivos:
#===============================================================================
# a) Apresentar os recursos gráficos básicos do R
# b) Documentação e ajuda
# c) Funções elementares
# d) Estruturas de dados
# e) Operadores
# f) Estruturas de controle de fluxo
# g) Funções
#===============================================================================

#===============================================================================
# Exemplos
#===============================================================================
demo()

demo(package = .packages(all.available = TRUE))
demo(graphics)  # Recursos gráficos genéricos
                # Para teclar <Enter> to see next plot:
                # é necessário que a tela esteja ativa

demo(image)     # Recursos gráficos 2D
demo(persp)     # Recursos gráficos 3D

library(lattice)
demo(lattice)   # Recursos gráficos

demo(glm.vr)    # Método lineares generalizados
demo(lm.glm)    # Lineares e lineares generalizados

#===============================================================================
# Documentação e ajuda
#===============================================================================
?round
?'for'  # ou ?”for“
?'[['   # ou ?”[[“
apropos('stem')
help.search('stem')
help.start()     # ou menu 'Help/Html help
vignette()       # documentos em pdf (dependente dos pacotes instalados)
vignette('grid') # abre pdf relacionado ao pacote grid

#===============================================================================
# Algumas funções elementares
#===============================================================================
set.seed(25)
x = round(runif(n = 20, min = 0, max = 10), digits = 2)
x
sort(x)
min(x)
max(x)
median(x)    # mediana
mean(x)      # média
var(x)       # variância
sd(x)        # desvio padrão (standard deviation)
sqrt(var(x))
sum(x)       # somatório
length(x)    # número de elementos
round(x, digits = 1)
round(x)
fivenum(x)   # Returns Tukey's five number summary (minimum, lower-hinge, median, upper-hinge, maximum)
quantile(x)  # quantis
quantile(x, c(0, .33, .66, 1))
cummax(x)
cummin(x)
plot(x, sin(x/20))
cor(x, sin(x/20))


# Imprimir no console uma mensagem ou o valor de uma variável:
print('Teste:')
x = 10
print(x)

# Concatenação:
cat('\nValor de x =', x); cat('\n')
cat('\n\tValor de x =', x); cat('\n')

#===============================================================================
# Estruturas de dados: MUITO IMPORTANTE!!!
#===============================================================================

#===============
# Vetores
#===============

# Algumas das diversas maneiras de defini-los:
c(1, 2, 3, 4, 5)
1:6
seq(1, 10, by = 1)
seq(1, 2, length = 10)
letters[1:5]
LETTERS[1:5]

# Algumas maneiras de recuperá-los:
x = seq(1, 10, by = 1)
x
x[5:10]
x[c(5, 7:10)]
x[-(5:10)]
x > 5
x[x > 5]
x[x < 6]

# Dar nomes aos componentes de um vetor:
names(x)
names(x) = letters[1:length(x)]
x
x['b']
c(a = 1, b = 5, c = 10)

# Algumas operações básicas:
set.seed(3)
x = round(runif(5, 0, 10), d = 1)
x
x/2
x*2
x+10
sort(x)
rev(sort(x))

set.seed(16)
x = sample(1:5, 10, replace = T)
x
sort(x)
unique(x)

x = c(1, 3, 2, 8, 5)
x
o = order(x)
o
x
x[o[1:3]]

#===============
# Matrizes
#===============
m = matrix(c(1, 2, 3, 4), nrow = 2)
m
m[1,2]

# O produto matricial:
x = matrix(c(6, 7), nrow = 2)
x
m %*% x

# O determinante de uma matriz:
det(m)

# A transposta de uma matriz:
t(m)

# Uma matriz diagonal:
diag(c(1,2))

# A identidade da matriz:
diag(1, 2)

diag(rep(1, 2))
diag(2)

# Comandos cbind e o rbind para criar matrizes:
cbind(c(1, 2), c(3, 4))
rbind(c(1, 3), c(2, 4))

# O traço de uma matriz:
sum(diag(m))

# A inversa de uma matriz :
solve(m)
solve(m, x)
solve(m) %*% x

# Autovalores:
eigen(m)$values

# Autovetores:
eigen(m)$vectors

# Certificar se a matriz é realmente diagonalisável:
p = eigen(m)$vectors
d = diag(eigen(m)$values)
p %*% d %*% solve(p)

#===============
# Arrays
#===============
ar = array(letters[1:24], c(2,4,3))
ar
ar[1,1,1] # ar[linha, coluna, dimensão] -> ar(x, y, z)
ar[1,1,2]
ar[1,2,3]

class(iris3)
iris3

#===============
# Fatores
#===============
set.seed(218)
x = factor(sample(c('a', 'b', 'c'), 5, replace = T))
x
l = c('d', 'e', 'f')
l
set.seed(17)
x = factor(sample(l, 5, replace = T), levels = l)
x
levels(x)

# Pode-se preferir uma tabela:
table(x)

# Se os valores estão de acordo com alguma razão, pode-se gerar níveis:
gl(1, 4)
gl(2, 4)
gl(2, 4, labels = c(T, F))
gl(2, 1, 8)
gl(2, 1, 8, labels = c(T, F))

# Pode fazer o produto cartesiano de dois fatores:
x = gl(2, 4)
x
y = gl(2, 1, length = 8)
y
interaction(x, y)

# O comando expand.grid é comparável (ele produz um frame), sendo muito útil para
# geração de níveis de fatores para as matrizes provenientes de dados
# experimentais:
a   = c('a1', 'a2', 'a3')
b   = c('b1', 'b2')
c   = c('c1', 'c2')
dad = expand.grid(a, b, c)
names(dad) = c('A', 'B', 'C')
dad

#===============
# Frames
#===============
n = 10
set.seed(17)
dF = data.frame(x = rnorm(n),
                y = sample(c(T, F), n, replace = T))
dF
# O comando str informa (retorna) a estrutura de um objeto e a parte dos dados
# que contém:
str(dF)

# Quando os objetos são armazenados, com sua própria ordem, o comando “unclass”
# da ordem pode alterá-lo:
n = 10
set.seed(3)
x = runif(n)
x
set.seed(19)
y = 1 - 2 * x + rnorm(n)
y
r = lm(y ~ x)
r
str(r)
r$coefficients
r$residuals
summary(r)

# A informação summary sumariza um objeto (aqui, um frame, mas vai bem com
# quase todos objetos):
summary(dF)
dF

# Pode-se ter acesso aos dados das colunas de diversas maneiras:
dF$x
dF[,1]
dF[['x']]
dim(dF)
names(dF)
row.names(dF)

# Ou pode-se mudar o nome das linhas ou das colunas:
names(dF) = c('a', 'b')
row.names(dF) = LETTERS[1:10]
names(dF)
row.names(dF)
str(dF)

# Pode-se ter acesso direto as colunas de um frame usando o comando attach().
# Obs: Não deve esquecer-se de destacá-lo detach() quando terminar:
data(faithful)
str(faithful)
attach(faithful)
str(eruptions)
detach()

#===============
# Listas
#===============
h = list()
h[['foo']] = 1
h[['bar']] = c('a', 'b', 'c')
str(h)

# Por exemplo, os parâmetros gráficos são armazenados em uma lista usada
# como contagens de chopping:
str(par())
h[['bar']] = NULL
str(h)

#===============
# Outros
#===============
# O comando split torna possível separar os dados de acordo com o valor
# de um fator:
n = 10
nn = 100
set.seed(21)
g = factor(round(n * runif(n * nn)))
x = rnorm(n * nn) + sqrt(as.numeric(g))
xg = split(x, g)
boxplot(xg, col = 'lavender', notch = TRUE, varwidth = TRUE)
str(xg)

# O comando apply torna possível aplicar uma função (para o exemplo, a média,
# quais, etc..) a cada coluna (ou linha) de um frame (ou de uma matriz):
options(digits = 4)
set.seed(5)
dF = data.frame(x = rnorm(20),
                y = rnorm(20),
                z = rnorm(20))
dF
apply(dF, 2, mean)
apply(dF, 2, range)

# Em dimensões mais elevadas:
options(digits=2)
set.seed(2)
m = array(rnorm(10^3), dim = c(10, 10, 10))
a = apply(m, 1, mean)
a
b = apply(m, c(1, 2), mean)
b
apply(b, 1, mean)

# A função tapply permite reagrupar as observações de acordo com o valor dos
# fatores e uma função (média, soma, etc..) para cada grupo obtido assim:
tapply(1:20, gl(2, 10, 20), sum)
by(1:20, gl(2, 10, 20), sum)

# A função sapply aplica a cada elemento de uma lista (ou de um vetor, etc..) e
# se possível retorna um vetor. A função lapply faz a mesma coisa, mas retorna
# uma lista:
x = list(a = rnorm(10),
         b = runif(100),
         c = rgamma(50, 1))
lapply(x, sd)
sapply(x, sd)

#===============================================================================
# Operadores
#===============================================================================
-5:7
set.seed(3)
x = floor(10*runif(10))
x
x[3]
x[1:3]
x[c(1, 2, 5)]

# O operador $ é reservado para recuperar um elemento de uma lista ou frame:
op = par()
op$col
op[['col']]
a = 'col'
op[[a]]

# A atribuição é feita por <- ou =.
x <- 1.17
x
y = c(1, 2, 3, 4)
y

# O produto de matrizes (% * %):
A = matrix(c(1, 2, 3, 4), nr = 2, nc = 2)
J = matrix(c(1, 0, 2, 1), nr = 2, nc = 2)
A
J
J %x% A

# O operador %o% é usado manufaturar tabelas da multiplicação
# (chama a função exterior com a multiplicação):
A = 1:5
B = 11:15
names(A) = A
names(B) = B
A %o% B

# A divisão euclidiana é %/%, seu restante é %%
1234 %% 3
1234 %/% 3
411*3 + 1

# A sociedade de uma 'unidade' é feita por %in%
17 %in% 1:100
17.1 %in% 1:100

# O operador ~ é usado descrever modelos (ANOVAS, métodos lineares, etc).
# Falaremos sobre ele mais tarde.
# Para mais detalhes (sobre os operadores negligenciados nestas notas)
# consulte o manual:
?'+'
?'<'
?'<-'
?'!'
?'['
?Syntax
?kronecker
?match
library(methods)
?slot

# Pode-se definir seus próprios operadores, pois são função diretas com dois
# argumentos cujo nome começa e as extremidades em %. O seguinte exemplo são
# tração do manual.

'%w/o%' = function(x, y) x[!x %in% y]
(1:10) %w/o% c(3,7,12)

#===============================================================================
# Estruturas de controle
#===============================================================================
set.seed(15)
x = rnorm(10)
x
y = ifelse(x > 0, 1, -1)
y
z = ifelse(x > 0, 1, ifelse(x < 0, '< zero', 0))
z

#===============
# Conexão:
#===============
set.seed(59)
x = letters[floor(1 + runif(1, 0, 4))]
x
y = switch(x,
           a='Bonjour',
           b='Gutten Tag',
           c='Hello',
           d='Konnichi wa')
y

#===============
# Loop for:
#===============
a = 0
for (i in 1:20) {
  a = i
  if(a <= 5 ) {
    cat('a = ', a, '(<= 5)'); cat('\n')
    next
  }
  if(a == 18) {
    cat('a = ', a, '(= 18)'); cat('\n')
    break
  }
}

#===============
# Loop while:
#===============
a = 0
while (a < 11) {
  if (a >= 3) print(a)
  else cat('não\n')
  a = a + 1  # expressão avaliada..
}

#===============
# Loop repeat:
#===============
a = 0
repeat {
  a = a + 1

  if (a >= 3) print(a)
  else cat('não\n')

  if (a == 10) break
}

#===============================================================================
# Funções
#===============================================================================
f = function(x) x/10 + 1

f(x = 10)
f(10)    # Chamada alternativa

f = function(x) {
  x/10 + 1
}

f(x = 10)
f(10)    # Chamada alternativa

# Pode atribuir valores aos argumentos:
f = function(x, y = 3) {
  x/10 + 1 - y
}

f(10)

# Na chamada da função, pode-se usar o nome dos argumentos, passar novos valores
# para as variáveis, não sendo necessário que os mesmos sigam a ordem declarada
# na função (desde que os valores sejam acompanhados dos respectivos nomes):
f(y = 1, x = 10)
f = function(x, y) {
    x/10 + 1 - y
}

f(1, 10)
f(10, 1)

# No fim dos argumentos, pode haver três pontos, representando todos os
# argumentos não especificados:
f = function(x, ...) {
  plot(x, ...)
}