Não foi possível enviar o arquivo. Será algum problema com as permissões?
Essa é uma revisão anterior do documento!
CE-227 - Primeiro semestre de 2014
No quadro abaixo será anotado o conteúdo dado em cada aula do curso.
São indicados os Capítulos e Sessões correspondentes nas referências bibliográficas,
bem como os exercícios sugeridos.
Veja ainda depois da tabela as Atividades Complementares.
Observação sobre exercícios recomendados os exercícios indicados são compatíveis com o nível e conteúdo do curso.
Se não puder fazer todos, escolha alguns entre os indicados.
Conteúdos das Aulas
| B & M | Online | |||
|---|---|---|---|---|
| Data | Conteúdo | Leitura | Exercícios | Tópico |
| 12/02 Qua | Teorema de Bayes: revisão, interpretações e generalização. Expressão probabilística de informação subjetiva, estimação baseada nos dados, estimação combinando informação prévia (subjetiva) e dados. Exemplo Binomial-Beta | Ver abaixo | Ver abaixo | |
| 14/02 Sex | Exemplo (cont). Inferência Bayesiana sobre parâmetro da Binomial com priori Beta. Determinação da posteriori | Ver notas de aulas Capítulos 1 e 2 | Exercícios dos Capítulos 1 e 2 das notas de aula | |
| 19/02 Qua | Discussão dos fundamentos do paradigma Bayesiano. Resumos e formas de explorar a posteriori: resumos pontuais e intervalares (intervalos de quantis e HPD). Inferência Bayesiana da distribuição Poisson-Gama | Ver notas de aulas Cap. 1 e 2 | Exercícios dos Capítulos 1 e 2 das notas de aula Ver abaixo | |
| 21/02 Sex | Discussão de possíveis soluções computacionais para especificação de prioris, resumos das posterioris incluindo intervalos HDP | Ver notas de aulas Capítulo 3 | Exercícios do Capítulo 3 das notas de aula | |
| 26/02 Qua | Avaliação semanal transferida devido a greve de ônibus. Explorando posterioris para prioris não conjugadas e que não possuem forma analítica conhecida. Métodos discutidos: (i) aproximação (Normal e Laplace) e (ii) amostragem da posteriori (aceitação/rejeição e MCMC) | Ver abaixo | ||
| 28/02 Sex | 1a Avaliação semanal (sabatina). Discussão da questão com destaque a resumos da posteriori. Especificação de Prioris: conjugadas, impróprias e "não informativas". Representações de ignorância e priori de Jeffreys. | Notas de aula, Cap. 3 | Ver abaixo | |
| 05/03 Sex | Feriado Carnaval | |||
| 07/03 Sex | 2a Avaliação semanal (sabatina). Resultados assintóticos e aproximação normal da posteriori. Algorítmo MCMC. | Notas de aula, Cap 7 | Ver abaixo | |
| 12/03 Qua | Predição bayesiana. Inferência para vetor de parâmetros. | Cap 4, Cap 6 | ||
| 14/03 Sex | Discussão sobre princípios e métodos bayesianos. Algorítmo de Gibbs. | |||
| 19/03 Qua | Princípio da verossimilhança. Histórico e contraste entre paradigmas para inferência | |||
| 21/03 Sex | 3a Avaliação semanal (sabatina). Revisão sobre métodos para obter e fazer inferências com posteriori: analítico (conjugado ou não), numérico, aproximação discreta, aproximação Gaussiana, simulação. Reparametrização e efeitos em aproximações e algoritmos de simulação. | Ver abaixo | ||
| 26/03 Qua | Priori's definidas por misturas, prioris de referências e para modelos de locação ou escala. Resumos pontuais e funções perda. Comentários sobre a questão da 3a avaliação. | Ver abaixo | ||
| 29/03 Sex | Discussão sobre a questão de 3a avaliação semanal | Ver abaixo | ||
| 02/03 Qua | Computação da questão de 3a avaliação semanal. Análise Bayesiana de dados: modelos linerares (Gaussianos). Construção do algorítmo de Gibbs | Ver abaixo | ||
12/02
- Procurar materiais introdutórios sobre inferência Bayesiana na web, livros, etc
- Escrever um programa que encontre os parâmetros da distribuição Beta a partir de estimativas pontuais, intervalos e respectiva probabilidade (como visto na aula)
- Investigar como foram encontrados os parâmetros na distribuição que combina dados e informações subjetivas mostrada em aula.
Seguem alguns resultados obtidos com meu código para encontrar os parâmetros da priori beta a partir de um valor que considera-se ser a moda, uma faixa de valores e uma probabilidade associada a esta faixa
| Opinião | Parâmetros da Priori | Parâmetros da Posteriori | Credibilidade (95%) | Credibilidade (95%) | ||||
|---|---|---|---|---|---|---|---|---|
| Escolha | Moda | Intervalo | alfa | beta | alfa* | beta* | quantis | HPD |
| 1 | 0.20 | [0.15 , 0.35] | 3.24 | 9.95 | 27.24 | 65.95 | [0.20 , 0.39] | [0.20 , 0.38] |
| 2 | 0.40 | [0.10 , 0.70] | 3.84 | 5.25 | 27.84 | 61.25 | [0.22 , 0.41] | [0.22 , 0.41] |
| 3 | 0.40 | [0.38 , 0.42] | 33.67 | 50.00 | 57.67 | 106.00 | [0.28 , 0.43] | [0.28 , 0.43] |
| 4 | 0.60 | [0.55 , 0.65] | 74.59 | 50.00 | 98.50 | 106.00 | [0.41 , 0.55] | [0.41 , 0.55] |
| 5 | 0.50 | [0.20 , 0.80] | 2.06 | 2.06 | 26.06 | 58.06 | [0.22 , 0.41] | [0.21 , 0.41] |
| 6 | 0.65 | [0.50 , 0.90] | 21.01 | 11.78 | 45.01 | 67.78 | [0.31 , 0.49] | [0.31 , 0.49] |
19/02
- Considere o exemplo visto em aula (lembrando que consideramos n=80 e y=24) e a sua escolha de priori e mostre como obter resumos pontuais da posteriori do modelo Binomial-Beta de duas formas distintas:
- usando resultados analíticos da distribuição,
- através de algum algorítmo computacional.
- Mostrar como obter intervalos de quantis e HPD para posteriori do modelo Binomial-Beta. Escrever rotinas computacionais e obter resultados para o exemplo de aula.
- Repetir anteriores para o modelo Poisson-Gama
26/02
- Obter amostras das posterioris nos modelo Binomial-Beta e Poisson-Gama. Extrair resultados e comparar com os analíticos obtidos anteriormente.
- Obter a aproximação de Normal para as posterioris destes dois modelos
- Escrever um algoritmo MCMC para obter amostras destes dois modelos (supondo - artificialmente - que a posteriori não é de forma conhecida).
28/02
- Refazer a questão da 1a avaliação.
- Encontrar a aproximação de Normal para a posteriori da questão da 1a avaliação. Fazer gráfico sobrepondo as distribuições, comparar resumos descritivos das distribuições. Avaliar a aproximação.
- Reconsidere a questão da 1a avaliação utilizando o parâmetro de precisão
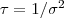 . Encontre a priori correspondente à definida (por transformação de variáveis).
. Encontre a priori correspondente à definida (por transformação de variáveis). - Mostre que para questão da 1a avaliação a distribuição gama inversa é conjugada. Idem para distribuição gama para o parâmetro de precisão.
- Considere agora a distribuição indexada para parâmetro (reparametrização)
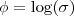 . Encontre a priori equivalente na definida na avaliação, encontre a distribuição a posteriori e a aproximação da Laplace correspondente. Sobreponha em um gráfico e discuta.
. Encontre a priori equivalente na definida na avaliação, encontre a distribuição a posteriori e a aproximação da Laplace correspondente. Sobreponha em um gráfico e discuta. - Monte um algoritmo MCMC para amostrar de algumas das posterioris da avaliação ou itens anteriores. Sobreponha em um gráfico a densidade obtida e a estimada pelas amostras MCMC. Transforme os valores simulados de acordo com as transformações dos itens anteriores e novamente compare graficamente as posterioris obtidas analiticamente e pelas simulações.
07/03
- Obter a aproximação normal para os exemplos vistos até agora no curso (modelos Poisson, Geométrico, Binomial Negativo, Binomial, Expoencial, Gamma, …)
- Montar um algorítmo MCMC para os exemplos vistos até agora no curso (modelos Poisson, Geométrico, Binomial Negativo, Binomial, Exponencial, Gamma, …)
21/03
- Considerar o problema da 3a avaliação semanal. Resolver analicamente e por métodos numéricos.
26/03
- Considere o modelo binomial e uma amostra com n=15 e y=6. Obtenha os gráficos da "trinca" priori, verossimilhança e posteriori nos seguintes casos:
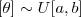
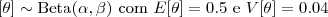
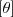 : priori de Jeffrey's
: priori de Jeffrey's
29/03
- Implementar algorítmos de inferência para o problema da 3a avaliação semanal. Fazer gráficos das quantidades e funções de interesse.
02/04
- Obter as expressões analíticas das posterioris conjunta, marginais e condicionais
do modelo de regressão linear com as prioris de referência.
- Estender o código a seguir (visto em aula) para comparar os resultados analíticos com os obtidos pelo amostrador de Gibbs. Incluir na comparação as distribuições e resumos pontuais e intervalares.
- Generalizar os resultados analíticos e códigos para priori Normal-InversaGamma
## simulando dados
x <- sort(runif(20, 0, 20))
y <- 2 + 0.25*x + rnorm(20, m=0, sd=2)
## visualizando dados e reta de regressão "usual"
plot(x,y)
reg <- lm(y ~ x)
abline(reg)
## Código ("ingênuo") para amostrador de Gibbs
reg.lin.GIBBS <- function(y, x, Nsim, iniBeta){
require(MASS)
n <- length(y)
X <- cbind(1, x)
XX <- crossprod(X)
bhat <- solve(XX,crossprod(X,y))
##
sim <- matrix(0, nrow = Nsim, ncol=3)
sim[1,1:2] <- iniBeta
sim[1, 3] <- 1/rgamma(1, shape=(n-2)/2, scale=2/crossprod(y-X%*%sim[1,1:2]))
for(i in 2:Nsim){
sim[i, 3] <- 1/rgamma(1, shape=(n-2)/2, scale=2/crossprod(y-X%*%sim[(i-1),1:2]))
sim[i,1:2] <- mvrnorm(n=1, mu=bhat, Sigma = solve(XX)*sim[i, 3])
}
return(sim)
}
## Obtendo amostras
rlG0 <- reg.lin.GIBBS(y=y, x=x, Nsim=15000, iniBeta=c(0,0.6))
## Burn-in (3000) e thining (1/10)
rlG1 <- rlG0[-(1:3000),]
rlG2 <- rlG1[10*(1:1200),]
## comparando estimativas "usuais" e médias das posterioris
c(coef(reg), summary(reg)$sigma^2)
apply(rlG2, 2, mean)
## traços e posterioris (por simulação) com indicação das estimativas "usuais"
par(mfrow=c(2,3))
plot(rlG2[,1], type="l")
plot(rlG2[,2], type="l")
plot(rlG2[,3], type="l")
plot(density(rlG[,1])); abline(v=coef(reg)[1])
plot(density(rlG[,2])); abline(v=coef(reg)[2])
plot(density(rlG[,3])); abline(v=summary(reg)$sigma^2)
04/04
- Estender os códigos anteriores para incluir a predição de novos valores