Essa é uma revisão anterior do documento!
Tabela de conteúdos
Probabilidades
Introdução
Na semana anterior, foram enfatizados alguns conceitos relacionados à estatística descritiva . Nesta semana, será apresentada a base teórica para muitas técnicas estatísticas de caráter inferencial.
Para entender a motivação em estudar o cálculo de probabilidades, imagine que um pesquisador selecione uma amostra de pacientes e registrou a idade e pressão arterial. Com base nesta amostra, ele identificou uma relação entre estas duas variáveis. O pesquisador pensa em estender as conclusões do seu estudo para outros pacientes, ou seja, fazer inferência. Neste exemplo específico, cabe a pergunta: a relação entre pressão e idade encontrada se deu ao acaso, ou há fortes indícios de que ela seja verdadeira ? A resposta à esta pergunta estará baseada no cálculo de probabilidades.
O cálculo de probabilidades é um importante ramo da teoria matemática, desenvolvido a partir da resolução de problemas em jogos de azar, que se destina a estudar fenômenos aleatórios. Estes fenômenos representam situações ou acontecimentos sobre os quais não há como predizer seus resultados. O cotidiano está repleto de fenômenos aleatórios. Veja por exemplo o resultado do lançamento de uma moeda, o tempo de espera em uma fila de banco e o retorno de um investimento de rentabilidade variável. Em todas estas situações, não é possível predizer com absoluta certeza qual será o resultado final.
Espaço Amostral
O conjunto Ω de todos os possíveis resultados de um fenômeno aleatório é chamado espaço amostral.
Veja alguns exemplos de fenômenos aleatórios e espaços amostrais:
- Lançamento de um dado honesto: Ω={1,2,3,4,5,6}
- Lançamento de uma moeda honesta: Ω={cara,coroa}
- Horário de ocorrência de queda de energia durante o dia Ω=(0h,24h)
Nos exemplos acima, os dois primeiros conjuntos são finitos, enquanto o terceiro contém infinitos elementos,por se tratar de um intervalo. Esta será uma importante classificação para os espaços amostrais: finitos e infinitos.
Veja a lista de outros fenômenos aleatórios presentes em nosso cotidiano.
Eventos
Os subconjuntos de Ω são chamados de eventos e, geralmente, representados por letras maiúsculas do alfabeto; A,B,C,…
Considere alguns eventos relacionados aos espaços amostrais descritos anteriormente:
- Evento A: Números pares obtidos em um lançamento de dado honesto.
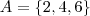
- Evento B: Números primos obtidos em um lançamento de dado honesto.
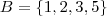
- Evento C :Horário de ocorrência de queda de energia no período da manhã situado entre 6:00h as 12:00h
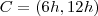
, alternativamente:
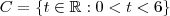
Ressalta-se que ao lidarmos com eventos, estamos lidando com conjuntos e, por isto, é importante conhecimento sobre a Teoria dos Conjuntos, principalmente suas operações básicas (união, interseção,complemento,…).
Alguns importantes conceitos na Teoria dos Conjuntos
Probabilidade
É uma função P(.) que associa números reais aos elementos do espaço amostral e satisfaz os 3 axiomas:
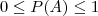
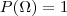
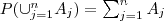 para
para 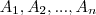 disjuntos.
disjuntos.
Dois eventos A e B são disjuntos se A ∩ B = ∅
A função P(.) faz um mapeamento de conjuntos em números reais.
Uma importante questão é a atribuição das probabilidades aos elementos do espaço amostral. Duas abordagens são comuns: atribuição a priori e a posteriori.
A priori :Considere um espaço amostral com n eventos elementares
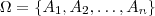
caso não haja justificativas para atribuir maior probabilidade a um determinado ponto, é natural imaginar que as chances estão igualmente distribuídas nestes n eventos e, portanto:
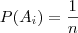
para i=1,2,…,n.
A atribuição de probabilidades a priori é feita quando se há conhecimento sobre as características físicas do experimento, como por exemplo no lançamento da moeda e do dado. Por outro lado, se não há conhecimento sobre as chances do eventos no espaço amostral, as probabilidades são atribuídas após repetidas observações do fenômeno aleatório.
Exemplo: Ao lançar um dado e observar o resultado obtido na face superior, as características físicas do experimento nos levam a atribuir probabilidades do seguinte modo:
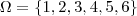
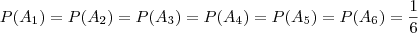
e nesta situação, as probabilidades são atribuídas a priori.
A posteriori : Quando não há conhecimento a priori das probabilidades, elas podem ser atribuídas através da experimentação. Observe o exemplo abaixo:
Exemplo: Seja a inspeção de peças em um processo de fabricação e os seguintes eventos A={Peça Defeituosa} e B ={Peça Perfeita}. Após inspecionar 1000 peças, verificou-se que 350 eram defeituosas. A partir deste experimento, ao selecionar aleatóriamente uma peça, pode-se atribuir as seguintes probabilidades:
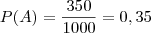
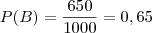
que são calculadas a posteriori, pela frequência de situações favoráveis em relação aos casos possíveis.
Regra da Adição de Probabilidades
A probabilidade da união de eventos é calculada através da regra da adição conforme a equação abaixo.

Probabilidade Condicional e Independência
Existem situações em que a ocorrência de um determinado evento B altera a chance de ocorrência de outro evento A. A informação da ocorrência do evento B traz um ganho de informação e a probabilidade de A pode ser "recalculada".
A probabilidade condicional é definida conforme a equação abaixo :
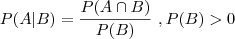
É comum a leitura da expressão acima como "probabilidade de A dado (a ocorrência) B".
Regra do Produto de Probabilidades
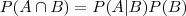
Independência de Eventos

Se a ocorrência do evento B não altera a probabilidade de ocorrência do evento A, os eventos A e B são ditos serem independentes. A partir dos resultados apresentados acima, torna-se direta a verificação de que:
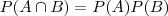
se A e B são eventos independentes.
Exemplo: Sejam dois lançamentos consecutivos de uma moeda honesta e a observação das faces superiores. Considere os eventos A={cara no primeiro lançamento} e B={cara no segundo lançamento}. Pelas características deste experimento, o resultado do primeiro lançamento não deve causar interferência na probabilidade de ocorrência de cara no segundo lançamento. De fato A e B são independentes e, portanto:
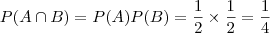
Veja o artigo : Entendendo Probabilidades Condicionais
Na área biológica existem vários exemplos de eventos dependentes e eventos independentes. Assim, olhos claros e cabelos claros são dois eventos dependentes porque a probabilidade de uma pessoa ter olhos claros é maior se a pessoa tem cabelos claros. Já "olhos claros" e "idade avançada" são eventos independentes pois um não modifica a probabilidade do outro.
Partição do Espaço Amostral
No Cálculo de Probabilidades, um conjunto de eventos que sejam mutuamente exclusivos entre si, ou seja, não tenham interseção e cuja união gere o espaço amostral irá constituir uma partição do espaço amostral. No trivial exemplo do lançamento de um dado honesto e observação da face superior, os eventos:
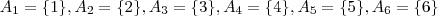
formam uma partição trivial do espaço amostral. Eles não tem interseção entre si, ou seja, não posso obter ao mesmo tempo 1 e 6 no lançamento de um dado, e a união entre eles reconstitui o próprio espaço amostral.
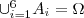
Para o mesmo fenômeno aleatório (face superior no lançamento de um dado honesto) existem outras formas de particionar o espaço amostral. Verifique, por exemplo, os eventos :
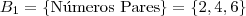
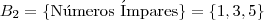
também formam uma partição do espaço amostral pois :
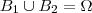
- não há interseção entre eles
Caso haja conhecimento das probabilidades dos eventos que formam a partição, este fato pode auxiliar o cálculo de probabilidades de outros eventos conforme o exemplo abaixo.
Exemplo: Em um determinado banco, 20 % dos clientes pertencem à classe social A, 40 % à classe social B, 20 % à C e o restante à classe D. Portanto, Considerando os eventos: A = {pertencer a classe social A}, B={pertencer a classe social B}, C = {pertencer a classe social C} e D = {pertencer a classe social D}.: P(A)=0,20;P(B)=0,40;P(C)=0,20;P(D)=0,20 a situação de inadimplência ocorre nas classes sociais de acordo com os seguintes percentuais :
Tabela 2.1 - Inadimplência dentro das classes sociais
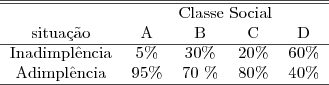
As informações desta tabela correspondem à probabilidades condicionais. Condicional ao fato de que o cliente pertence a classe A, sua probabilidade de inadimplência é 0,05.
Com estes dados, qual a probabilidade de sortear um cliente inadimplente ?
Note que no exemplo acima, as classes sociais formam a partição do espaço amostral constituído pelos clientes do banco. As probabilidades de cada elemento da partição também são conhecidas, mas a probabilidade de um cliente ser inadimplente, independentemente de sua classe social, ainda não é conhecida, devendo ser calculada.
Considere o evento 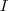 = {cliente inadimplente}. O cliente inadimplente deve obrigatoriamente pertencer a uma das classes sociais e, não pode pertencer a mais do que uma. Logo, a probabilidade de
= {cliente inadimplente}. O cliente inadimplente deve obrigatoriamente pertencer a uma das classes sociais e, não pode pertencer a mais do que uma. Logo, a probabilidade de 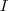 pode ser expressa como :
pode ser expressa como :
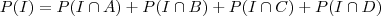
Entretanto, pela definição de probabilidade condicional, podemos re-expressar a probabilidade acima como:
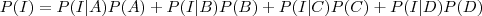
As probabilidades acima são todas conhecidas pois 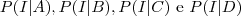 são probabilidades de inadimplência condicionais ao conhecimento da classe social e foram fornecidas na Tabela 2.1.
são probabilidades de inadimplência condicionais ao conhecimento da classe social e foram fornecidas na Tabela 2.1.
Substituindo as respectivas probabilidades, a probabilidade de inadimplência será:
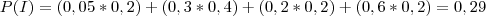
Conforme o cálculo acima, a probabilidade de sortear um cliente e este ser inadimplente é de 29 %.
A solução do problema acima, calcular a probabilidade de sortear este cliente e este ser inadimplente, foi encontrada mediante a utilização do chamado Teorema da Probabilidade Total. Abaixo enunciamos este teorema.
Teorema da Probabilidade Total
Seja uma partição do espaço amostral 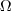 :
:
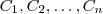
Para qualquer evento A pertencente a este espaço amostral, podemos escrever sua probabilidade como :
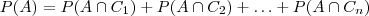
e usando a definição de probabilidade condicional;
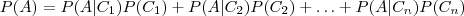
Teorema de Bayes
A razão entre as probabilidades condicionais é a mesma razão entre as probabilidades incondicionais.
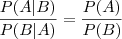
Este resultado é geralmente expresso como:
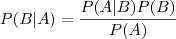
Considere uma partição C1,C2,…,Cn do espaço amostral Ω. A probabilidade condicional de um determinado elemento desta partição pode ser escrita como:
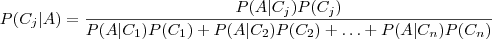
que corresponde a enunciação geral do Teorema de Bayes.
Veja aplicação de probabilidade em saúde: Avaliação da qualidade de testes diagnósticos