Não foi possível enviar o arquivo. Será algum problema com as permissões?
Essa é uma revisão anterior do documento!
CE-003: Estatística II
Detalhes da oferta da disciplina
- Período: Turma B (Engenharia Civil), primeiro semestre de 2011.
- Professor Responsável: Walmes Marques Zeviani, (LEG: Laboratório de Estatística e Geoinformação)
- Horário e Local: terças e quintas, 15:30 - 17:30, Sala PF-03
- Data importantes:
- 28/08/2011 - Início das aulas
- 26/06/2011 - Último dia letivo do 2o semestre
- 04/07 a 09/07/2011 - Período de exames finais
- Calendário completo: Resolução 71/10 do CEPE que estabelece o calendário para ano de 2011 (formato PDF)
- Avaliação: serão realizadas 3 provas (conteúdo e datas a definir):
- Horários de atendimento do Professor : Segundas e quartas, 16:30 - 17:30, LEG (Laboratório de Estatística e Geoinformação), prédio anexo ao prédio da administração do centro politécnico, andar superior (espaço do antigo salão de provas)
Programa/Objetivos da Disciplina
O objetivo desta disciplina é capacitar os alunos em conceitos básicos de estatística que permitam a interpretação de resultados de análises e procedimentos estatísticos bem como a execução de procedimentos e análises estatística básicas. O curso compreende três grandes tópicos:
- Análise descritiva e exploratória de dados
- Noções de probabilidades e distribuições de probabilidades
- Introdução à procedimentos de inferência estatística
Acesse a ementa da disciplina.
Referências Bibliográficas
- Referências básicas
- MAGALHÃES, M.N.; LIMA, A.C.P. (2004)Noções de Probabilidade e Estatística. 6ª edição. IME/SP. Editora EDUSP.
- ANDRADE, D.F; OGLIARI, P.J. (2007) Estatística para as Ciências Agrárias e Biológicas (com noções de experimentação). Editora da UFSC
- BARBETTA, P.A.; REIS, M.M.; BORNIA, A.C. (2004) Estatística para cursos de engenharia e informática. Editora Atlas.
- Referências complementares:
- DANTAS, C.A.B. (2008) Probabilidade: um curso introdutório. 3a Edição revista. Editora Edusp.
- MAGALHÃES, M.N. Probabilidades e variáveis aleatórias. Editora Edusp. (Capítulos 1 e 2).
- MORGADO, A.C.O., CARVALHO, J.B.P., CARVALHO, P.C.P. & FERNANDEZ, P. (1991) Análise Combinatória e Probabilidade. Soc. Bras. de Matemática.
- MONTGOMERY, D.C. & RUNGER, G.C. Applied statistics and probability for engineers. Wiley.
- MONTGOMERY, D.C. & RUNGER, G.C. Estatística aplicada e probabilidade para engenheiros. (2003) LTC Editora. (esta é uma tradução da referência anterior)
- PETER DALGAARD. (2002) Introductory Statistics with R. Springer.
- Nota: existem diversos textos de estatística compatíveis com o programa do curso. Consulte o professor sobre a adequação de qualquer outra referência bibliográfica.
- Leituras complementares
- Marques de Sá, J. (2006) O Acaso - o jogo da vida e a vida dos jogos. Ciência Aberta.
- Colin Bruce (2003) Novas aventuras científicas de Sherlock Holmes (Casos de lógica, matemática e probabilidade). Jorge Zahar Editora.
- Daniel Kehlmann (2007) A medida do mundo. Companhia das Letras.
Materiais do Curso
ATENÇÃO: estes arquivos/página poderão ser atualizados durante o curso.
Histórico das Aulas do Curso
Abaixo o histórico de atividades realizadas em classe e atividades extra classe sugeridas.
Legenda:
- (M&L) MAGALHÃES, M.N.; LIMA, A.C.P. (2004)Noções de Probabilidade e Estatística. 6ª edição. IME/SP. Editora EDUSP.
- (B,R&B) BARBETTA, P.A.; REIS, M.M.; BORNIA, A.C. (2004) Estatística para cursos de engenharia e informática. Editora Atlas.
| Data | Classe | Extra |
|---|---|---|
| ter 01/Mar (aula 0) | Esclarecimento sobre local, horários das aulas, bibliografia de referência, métodos de avaliação, datas das avaliações, horário e local do plantão de dúvidas, controle de presença, divulgação das notas, faltas, atividades e página web da disciplina. | Visitar a página da disciplina. |
| qui 03/Mar (aula 1) | Probabilidades: fenômeno aleatório, espaço amostral, eventos, união, intersecção, definição de probabilidade, probabilidade condicional, independência. | Ler capítulo 2 (M&L), capítulo 4 (B,R&B), capítulo 5 (B&M) e fazer exercícios correspondentes. |
| ter 08/Mar (aula -) | Recesso de Canaval | - |
| qui 10/Mar (aula 2) | Teorema da probabilidade total e teorema de Bayes, resolução dos exercícios 4, 8, 10 do B,R&B, das páginas 101, 110, 113. | Ler capítulo 4.4-4.5 (B,R&B), capítulo 5.4 (B&M) e fazer exercícios correspondentes. |
| ter 15/Mar (aula 3) | Variáveis aleatórias, caso discreto, função distribuição de probabilidades, valor médio, variância, propriedades. | Ler capítulo 6.0-6.5 (B&M) e fazer exercícios correspondentes. |
| qui 17/Mar (aula 4) | Função distribuição de probabilidades. Modelos probabilísticos para variáveis aleatórias discretas: uniforme, Bernoulli, binomial e Poisson. | Ler capítulo 6 (B&M), capítulo 5 (B,R&B) e fazer exercícios correspondentes. |
| ter 22/Mar (aula 5) | Diferenças entre variáveis aleatórias discretas e contínuas. Modelos probabilísticos para variáveis aleatórias contínuas: uniforme contínua, normal e exponencial. | Baixar e tomar conhecimento da tabela de distribuição de probabilidades Normal (Tabelas Estatísticas (distribuições de probabilidade)). Ler capítulo 7.0-7.4 (B&M), capítulo 6 (B,R&B) e fazer exercícios correspondentes. |
| qui 24/Mar (aula 6) | Resolução de exercícios sobre variáveis aleatórias e modelos probabilísticos discretos. Exercícios ex.1 p.135 B&M, ex.2 p.135 B&M, ex.3 p.135 B&M, ex.7 p.136 B&M, ex.10 p.139 B&M, ex.7 p.131 B,R&B, ex.11 p.136 B,R&B. | Fazer os demais exercícios relacionados à esse tópico. |
| ter 29/Mar (aula -) | Não houve aula pois o Docente estava participando de curso de capacitação ministrado por Edzer Pebesma. Foi marcada a primeira avaliação para o dia 28/04/11. | Carpe diem. |
| qui 31/Mar (aula 7) | Como consultar a tabela da distribuição Normal (finger's rule e inverse finger's rule) e resolução de exercícios sobre variáveis aleatórias e modelos probabilísticos contínuos. Exercícios ex.1 p.167 B&M, ex.2 p.167 B&M, ex.6 p.172 B&M, ex.17 p.184 B&M. | Fazer os demais exercícios relacionados à esse tópico. |
| ter 05/Abr (aula 8) | Aproximação Normal à binomial. Estatística descritiva, objetivos, tipos de variáveis observadas, representação tabular e gráfica da distribuição de frequências. | Ler o capítulo 2.0-2.3 (B&M), ler capítulo 3.0-3.3 (B,R&B) e fazer exercícios correspondentes. |
| qui 07/Abr (aula 9) | Cálculo da distribuição de frequência absoluta/relativa/acumulada, gráfico de distribuição de frequências (histograma) absoluta/relativa/acumulada, gráfico de setores, distribuição acumulada empírica, diagrama de ramos e folhas, gráfico de densidade suavizada. | Todos os gráficos foram feitos com o aplicativo estatístico R (clique para download) e os comandos estão disponíveis no aquivo aula1.R e os dados no arquivo notasfinais2.txt. |
| ter 12/Abr (aula 10) | Procedimento para construção do diagrama de ramos e folhas, tabela e gráfico de distribuição de frequência. Medidas de posição: média, mediana e moda (para dados não agrupados e agrupados). Medidas de dispersão: desvio médio, variância e desvio padrão. Uso do modo estatístico na calculadora CASIO fx-82MS. | Ler capítulo 2-3 (B&M), capítulo 3 (B,R&B). Fazer exercícios correspondentes. |
| qui 14/Abr (aula 11) | Variância para dados agrupados, separatrizes, cálculo dos quartis, amplitude total e interquartílica, interpretação do gráfico de caixas e bigodes (boxplot), medidas de forma, interpretação e cálculo dos coeficientes de assimetria e curtose. | Ler capítulo 2-3 (B&M), capítulo 3 (B,R&B). Fazer exercícios correspondentes. |
| ter 19/Abr (aula 12) | Análise bidomensional, medidas de associação entre e gráficos para visualização de duas variáveis, casos qualitativa-qualitativa, quantitativa-quantitativa, quantitativa-qualitativa. | Ler capítulo 4 (B&M) e fazer exercícios correspondentes. Material usado na aula foi o arquivo de procedimentos aula2.R e o arquivo de dados alfab-renda.txt. |
| qui 21/Abr | Não haverá aula devido ao feriado. | Estudar para a prova. |
| ter 26/Abr | Não haverá aula pois o docente estará ministrando Curso | Estudar mais um pouco para a prova. |
| qui 28/Abr | Primeira avaliação: probabilidade, variáveis aleatórias, modelos discretos e contínuos. | Começar a estudar para recuperar a nota da primeira prova. |
| ter 03/Mai (aula 13) | Foram feitos exercícios sobre o conteúdo relacionado à estatística descritiva. | Praticar/fazer exercícios relacionados à estatística descritiva e definir a data da segunda avaliação. |
| qui 05/Mai (aula 14) | Introdução à inferência estatística. Definição de população, amostra e parâmetros. Tipos de amostragem. Problemas de inferência estatística: estimação, teste de hipótese e previsão. | Ler capítulo 10 (B&M). Resultado do desempenho na primeira avaliação disponível. |
| ter 10/Mai (aula 15) | Estatísticas, parâmetros, distribuição amostral, teorema do limite central e distribuição amostral da média. | Ler capítulo 10.6-10.8 (B&M), capítulo 7.0-7.2 (B,R&B), capítulo 7.0-7.3 (M&L), fazer exercícios correspondentes. Rodar arquivo aula3.R. Data para revisão de prova disponível. |
| qui 12/Mai (aula 16) | Distribuição amostral da proporção, dimensionamento de amostra, introdução à estimação, propriedades de um estimador. | Ler capítulo 10.9-11.2 (B&M), capítulo 7.0-7.2,7.4 (B,R&B), capítulo 7.0-7.3 (M&L), fazer exercícios correspondentes. |
| ter 17/Mai (aula 17) | Métodos de estimação: momentos, mínimos quadrados e máxima verossimilhança. Definição de confiança, caso da média amostral. | Ler capítulo 11.0-11.6 (B&M), capítulo 7.3 (B,R&B), capítulo 7.2,7.4 (M&L), fazer exercícios correspondentes. |
| qui 19/Mai | Segunda avaliação: estatística descritiva, resumos gráficos e numéricos de dados. | Notas e data para revisão de prova disponível. |
| ter 24/Mai (aula 18) | Foram feitos exercícios sobre o conteúdo relacionado à distribuição amostral e intervalos de confiança. | Fazer exercícios relacionados a esse tópico. |
| qui 26/Mai (aula 19) | Intervalo de confiança para a variância populacional, distribuição qui-quadrado, teste de hipótese, tipos de erros, teste de hipótese para a média populacional. | Ler capítulo 12.0-12.5 (B&M), capítulo 8.0-8.6 (B,R&B), capítulo 8.0-8.2 (M&L), fazer exercícios correspondentes. |
| ter 31/Mai | ? | ? |
| qui 02/Jun | ? | ? |
| ter 07/Jun | ? | ? |
| qui 09/Jun | ? | ? |
| ter 14/Jun | ? | ? |
| qui 16/Jun | ? | ? |
| ter 21/Jun | ? | ? |
| qui 23/Jun | ? | ? |
| ter 28/Jun | Terceira avaliação: | ? |
| qui 30/Jun | ? | ? |
| ter 05/Jul | exame final (data definida pela Coordenação do Curso de Engenharia Cívil), todo conteúdo. | ? |
| qui 07/Jul | ? | ? |
Avaliações
| Data | Conteúdo | Prova | Gabarito | Notas | Revisão |
|---|---|---|---|---|---|
| (28/04/2011) | probabilidade, variáveis aleatórias, modelos discretos e contínuos. | desempenho-notas.pdf. | 13, 16, 18/05/2011 das 15-16:00 h, LEG. | ||
| (19/05/2011) | estatística descritiva, resumos gráficos e numéricos de conjuntos de dados. | desempenho-notas.pdf. | 25 e 30/05/2011 das 15-16:00 h, LEG. | ||
| (??/06/2011) | inferência estatística, estimação e testes de hipótese. | ||||
| (05/07/2011) | todo o conteúdo. |
Programas computacionais
O curso não prevê conteúdo computacional. Entretanto todo o conteúdo abordado pode ser tratado computacionalmente por planilhas eletrônicas (como por exemplo o OpenOffice) ou programas estatístico. O uso de programas computacionais pode auxiliar (e muito!) o entendimento do conteúdo do curso e não será parte da avaliação do curso.
- Programa estatístico recomendado
- The R project for Statistical Computing: página do programa R
- Recursos auxiliares
- Uma página interessante com um introdução ao R
- O Xemacs é uma outra opção de editor que facilita a edição de arquivos do
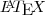e R e disponível para plataformas Linux e Windows. - R_STAT é uma lista de discussão em português sobre o uso do R no yahoo groups
