Não foi possível enviar o arquivo. Será algum problema com as permissões?
LCE-5715 - Métodos Computacionais para Inferência com Aplicações em R
O objetivo da disciplina é apresentar e discutir os principais métodos computacionais utilizados em inferência estatística. Prover complemento computacional para disciplinas do programa. Capacitar participantes a desenvolver algoritmos e escrever códigos com vistas a implementações de modelos e extensões não contempladas em implementações de software.
Programa Analítico
- Programação da função de verossimilhança para variáveis discretas, contínuas ou misturas.
- Programação do algoritmo de Newton Raphson.
- Programação do algoritmo Scoring de Fisher.
- Programação do algoritmo do tipo EM.
- Programação do algoritmo Gauss-Newton.
- Métodos de aproximação de integrais Monte Carlo, Boostraping.
- Exploração numérica da verossimilhança, verossimilhanças perfilhadas e marginais.
- Métodos para modelos com efeitos aleatórios.
- MCMC – Monte Carlo via Cadeias de Markov.
Detalhes da oferta da disciplina
- Período: segundo semestre de 2016, no programa de pós graduação de estatística e experimentação agronômica da ESALQ/USP
- Matrículas e informações: com Solange de Assis Paes Sabadin (
solange.sabadin) ou Mayara Segatto (ATusp.brmayarasegattoATgmail.com) na secretaria do programa, Telefone: (19) 3429-4144, ramal 231 - Professores Responsáveis:
- Roseli Aparecida Leandro (ESALQ/USP)
- Horários e Locais:
- As aulas serão na sala 311
- Horário: Sextas, 8:00 às 12:00
- Datas especiais:
12/08/2016 24/11/2016 Início das aulas Último dia de aula
Referências Bibliográficas
- Material básico: capítulos 1 a 5 de:
- Bonat et al. (curso do SINAPE/2012, pdf com versão atualizada)
- Materiais adicionais
- Albert, J. (2009) Bayesian Computation with R. Second Edition. New York: Springer.
- Braun, W. J. e Murdoch, D. J. (2007). A First Course in Statistical Programming with R. Cambridge University Press.
- Gamerman, D. e Lopes, H. F. (2006). Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. Second Edition. London: Chapman & Hall/CRC Press.
- McLachlan, G. e Krishnan, T. (1996). The EM Algorithm and Extensions. John Wiley & Sons, New York.
- Rizzo, M. (2008). Statistical Computing with R. CRC/Chapman Hall.
- Robert, C. e Casella, G. (2010). Introducing Monte Carlo Methods with R. New York: Springer.
- Robert, C. e Casella, G. (2004). Monte Carlo Statistical Methods (2a edição). Springer.
- Tanner, M.A.(1996). Tools for statistical inference methods for the exploration of posterior distributions and likelihood functions. Springer, New York.
- Venables, W. N. e Ripley, B. D. (2002) Modern Applied Statistics with S. Fourth Edition. New York: Springer-Verlag.
Materiais do Curso
ATENÇÃO: arquivos/páginas poderão atualizados durante o curso.
Programas computacionais
- Programa básico do curso
- The R project for Statistical Computing: página do programa R
- Recursos auxiliares
- Uma página interessante com uma introdução ao R
- R-Studio um ambiente para facilitar uso do R
- R-br é a lista de discussão em português sobre o uso do R
- Programas para matemática simbólica
-
-
- Interface do R com o Sympy
Histórico das aulas
| Dia | Conteúdo | Materiais | Comentário | Atividades |
|---|---|---|---|---|
| 12/08 | Apresentação do curso, professores e participantes. Introdução ao uso do programa R | Comandos do R | Profa Roseli, Paulinho remoto | |
| 16/09 | Inferência com verossimilhança | Slides do curso | Cap 1 e 2 do livreto | 16/09 |
| 07/10 | Inferência com dois (ou mais) parâmetros e modelos de regressão | Slides do curso | Cap 3 e 4 do livreto | 08/10 |
| 18/11 | Modelos de efeitos Aleatórios | Slides do curso | Cap 4 do livreto | 18/11 |
16/09
- Considere a distribuição exponencial
- Simular um conjunto de (15) dados
- Obter gráficos de verossimilhança, log-verossimilhança, verossimilhança relativa e função deviance para as 2 parametrizações usuais da exponencial
- Obter em cada caso IC's
- assintóticos para parametrição usada
- assintóticos de uma transformação transformados diretamente para outra
- assintóticos de uma transformação transformados (método delta) para outra
- por corte na função deviance (ou alguma outra)
- por corte na função deviance (ou alguma outra) e diretamente transformado para outra parametrização
- Fixar um valor arbitrátio e fazer testes da razão de verossimilhança, Wald e score
- Repetir problema anterior para outras distribuições (Poisson, Beta, Gamma etc). No caso de distribuição de 2 parâmetros, fixar um deles e fazer inferência sobre o outro.
- Verificar como foram feitos os cálculos de relação entre os "pontos de corte" para definição de intervalos baseados em verossimilhança mostrados na tabela do texto/slides do curso
- Alguns scripts:
08/10
- scripts mostrados em aula
18/11
- Simular dados do processo de Poisson homogêneo e não homogêneo e escrever e rodar funções de verossimilhança ppara estimar parâmetros
- Fazer passo a passo o modelo de regressão com efeitos eleatórios gaussiana, derivando a expressão da verossimilhança (marginal/integrada):
- no modelo de regressão simples com intercepto aleatório
- no modelo mmais geral (estrutura matricial
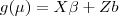
- Script do exemplo Poisson visto em aula
- extender o modelo do script para estrutura de regressão linear simples na média
Espaço Aberto
Página aberta para edição pelos participantes do curso.