CE-227 - Primeiro semestre de 2016
No quadro abaixo será anotado o conteúdo dado em cada aula do curso.
São indicados os Capítulos e Sessões correspondentes nas referências bibliográficas,
bem como os exercícios sugeridos.
Veja ainda depois da tabela as Atividades Complementares.
Observação sobre exercícios recomendados os exercícios indicados são compatíveis com o nível e conteúdo do curso.
Se não puder fazer todos, escolha alguns entre os indicados.
Conteúdos das Aulas
| Data | Conteúdo | Leitura | Exercícios | Tópico |
|---|---|---|---|---|
| 29/02 Seg | Teorema de Bayes: revisão, interpretações e generalização. Expressão probabilística de informação subjetiva, estimação baseada nos dados, estimação combinando informação prévia (subjetiva) e dados. Exemplo Binomial-Beta | Ver abaixo | ||
| 02/03 Qua | Conceitos e fundamentos da modelagem Bayesiana. Tipos e classificações de prioris. Posterioris analíticas, aproximadas e numéricas/amostragem. Comparações com abordagens não Bayesianas. Exemplo Binomial-Beta revisitado. | Ver abaixo | ||
| 07/03 Seg | Elicitação de priori. Exemplo Binomial-Beta revisitado. Algorítimo para obtenção de parâmetros da priori a partir de opinião subjetiva. Implementação condicional. Informações nas prioris/verossimilhanças e posterioris | Ver abaixo | ||
| 09/03 Qua | Aproximação normal da posteriori. Revisão de aproximação. Obtenção analítica e numérica. Exemplo computacional. Ilustração com Binomial-Beta | Ver abaixo | ||
| 14/03 Seg | Aproximação discreta da priori/posteriori. Obtenção da posteriori por amostragem. Métodos: amostragem por rejeição e MCMC | Ver abaixo | ||
| 16/03 Qua | Implementação computacional dos métodos descritos na aula anterior. | |||
| 21/03 Seg | Apresentação e discussão crítica das implementações computacionais. | |||
| 23/03 Qua | Discussão sobre Cap 1 do texto do curso. Paradigmas de inferência. | |||
| 28/03 Seg | Discussão sobre Cap 2 do texto do curso. | Exercícios do Capítulo | ||
| 30/03 Seg | Discussão sobre Cap 3 do texto do curso (prioris). | Exercícios do Capítulo | ||
| 04/04 Seg | Inferência (bayesiana e não bayesiana) sobre o parâmetro variância de uma distribuição normal (com média fixa). Revisão conceitual e comparações. | arquivo discutido em aula | ||
| 06/04 Qua | desenvolver análises análogas às vistas na última aula para algum outro modelo com 1 parâmetro (excluindo da binomial ou algum dos parâmetros da normal) | |||
| 11/04 Seg | Discussão das análises feitas pelos participantes do curso. Modelos com mais de um parâmetro - ideais fundamentais. Distribuições posterioris marginais, conjuntas e condicionais. | Cap 4 do material do curso | ||
| 13/04 Qua | Resumos da posteriori | Cap 5 do material do curso | Preparar material para discussão sobre FBST | |
| 18/04 Seg | Predição Bayesiana | Cap 6 do material do curso | Ver abaixo | |
| 20/04 Qua | Testes FBST - parte 1/2 | |||
| 25/04 Seg | Testes FBST - parte 2/2 e revisão/dúvidas para prova | |||
| 27/04 Qua | 1a prova | |||
| 02/05 Seg | Discussão da 1a prova | |||
| 04/05 Qua | Atividades dos alunos - revisão da prova | |||
| 09/05 Seg | Discussão da prova e detalhamento do problema da questão 5 | Ver abaixo | ||
| 11/05 Qua | Discussão Caps 7 e 8 do material | Ver abaixo | ||
| 16/05 Seg | Inferência Bayesiana utilizando o JAGS - instalação e exemplos | Ver abaixo | ||
| 18/05 Qua | Inferência Bayesiana utilizando o JAGS/INLA - mais exemplos | Ver abaixo | ||
| 23/05 Seg | Estudos (prof. em congresso) | |||
| 25/05 Qua | Estudos (prof. em congresso) | |||
| 31/05 Seg | Aplicação de inferência Bayesiana - erros e incertezas em estimação de vazão de uma bacia - Apres. Alana | |||
| 01/06 Qua | Fundamentos do INLA | Ver abaixo |
29/02
Manifestar uma opinião subjetiva sobre o parâmetro de uma distribuição binomial. (basear-se no contexto de intenção de voto discutido em aula)
02/03
Encontrar um algoritmo que especifique os parâmetros de uma distribuição Beta a partir da opinião subjetiva manifestada.
07/03
Encontrar a aproximação normal para a posteriori do exemplo beta-binomial
09/03
Propor e implementar um algorítimo para obtenção de amostras da posteriori do exemplo discutido no curso.
14/03
Propor e implementar algorítimos para discretização da posteriori e amostragem via métodos a rejeição e MCMC.
18/04
Considere o modelo de verossimilhança 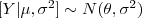 e a priori
e a priori 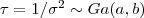 . Mostre como obter a densidade:
. Mostre como obter a densidade:
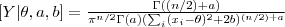 .
.
Como este resultado pode ser interpretado?
09/05
- Obter os resultados analíticos possíveis para o problema da questão 5 da prova (posteriori, constante de integração, aproximação quadrática, etc)
- Implementar os diferentes métodos para inferência baseada na posteriori (exata, aproximação normal, discretização, amostragem)
11/05
- Derivar os expressões das condicionais completas no problema do ponto de mudança da Poisson (ex. do capitulo 8)
- Implementar o algorítmo de Gibbs para este exemplo.
16/05
Exemplos discutidos utilizando JAGS/rjags:
- Amostragem da normal
## Simulando um conjunto de dados n <- 20 x <- rnorm(n, 70, 5) ## Exportar os dados (não é necessário) se utilizando o rjags #write.table(x, # file = 'normal.data', # row.names = FALSE, # col.names = FALSE) ## Especificação do modelo (deve ser exportada para um arquivo) cat( "model { for (i in 1:n){ x[i] ~ dnorm(mu, tau) } mu ~ dnorm(0, 0.0001) tau <- pow(sigma, -2) sigma ~ dunif(0, 100) }", file="normal.modelo" ) ## Carregando o pacotes rjags (pode-se ainda usar outros como runjags, R2jags etc) require(rjags) ## Definindo valores iniciais. No caso três conjuntos porque iremos rodas 3 cadeias. ## OBS: valores iniciais são dispensáveis neste exemplo inis <- list(list(mu=10, sigma=2), list(mu=50, sigma=5), list(mu=70, sigma=10)) ## O proximo comando prepara e " compila" o modelo e opções para o algorítmo jags <- jags.model('normal.modelo', data = list('x' = x, 'n' = n), n.chains = 3, inits = inis, n.adapt = 100) ## Obtendo as amostras (diferentes opções, a última já prepara em formato para uso com o ## pacote ´coda´) #update(jags, 1000) #sam <- jags.samples(jags, c('mu', 'tau'), 1000) sam <- coda.samples(jags, c('mu', 'tau'), n.iter=10000, thin=10) ## Visualizações e resultados par(mfrow=c(2,2)) plot(sam) str(sam) summary(sam) HPDinterval(sam) - regressão linear simples
## simulando dados n <- 20 x <- sort(runif(n, 0, 20)) epsilon <- rnorm(n, 0, 2.5) y <- 2 + 0.5*x + epsilon plot(y ~ x) lines(lm(y ~x)) ## especificando o modelo para o JAGS cat( "model { for (i in 1:n){ y[i] ~ dnorm(mu[i], tau) mu[i] <- b0 + b1 * x[i] } b0 ~ dnorm(0, .0001) b1 ~ dnorm(0, .0001) tau <- pow(sigma, -2) sigma ~ dunif(0, 100) }", file="reglin.modelo") ## poderia-se redefinir o modelo acima com uma possível priori alternativa, por ex: ## tau ~ dgamma(0.001, 0.001) ## sigma2 <- 1/tau #write.table(data.frame(X = x, Y = y, Epsilon = epsilon), # file = 'reglin.dados', # row.names = FALSE, # col.names = TRUE) require(rjags) ## Valores iniciais (vamos rodar só duas cadeias neste exemplo) inis <- list(list(b0=0, b1=1, sigma=1), list(b0=1, b1=0.5, sigma=2), list(b0=2, b1=0.1, sigma=5)) ## Compilando modelo, dados e opções jags <- jags.model('reglin.modelo', data = list('x' = x, 'y' = y, 'n' = n), n.chains = 2, # inits=inits, n.adapt = 100) #update(jags, 1000) class(jags) ## obtenção das amostras da posteriori ... ## ... via rjags sam <- jags.samples(jags, c('b0', 'b1', 'sigma'), 1000) class(sam) ## ... ou via coda sam <- coda.samples(jags, c('b0', 'b1', 'sigma'), 1000) class(sam) str(sam) plot(sam) ## Pode-se tb obter as distribuições preditivas correspondentes a cada observação sam <- coda.samples(jags, c('b0', 'b1', 'sigma', "y"), 1000) str(sam) int <- HPDinterval(sam) str(int) ## complementar com gráficos, resumos, inferências de interesse, etc - Coeficiente de correlação intraclasse
## Dados simulados do modelo: ## Y_{ij} \sim N(\mu_{i}, \sigma^2_y) ## mu_{i} = theta + b_{i} ## b_{i} \sim N(0, \sigma^2_b) ## que, por ser normal (com ligação identidade) ## pode ser escrito por: ## Y_{ij} = \beta_0 + b_{i} + \epsilon_{ij} ## ## simulando dados: Ngr <- 25 Nobs <- 10 set.seed(12) sim <- data.frame(id = Ngr*Nobs, gr = rep(1:Ngr, each=Nobs), bs = rep(rnorm(Ngr, m=0, sd=10), each=Nobs), eps = rnorm(Ngr*Nobs, m=0, sd=4) ) sim <- transform(sim, y = 100 + bs + eps) sim ## estimativas "naive" resumo <- function(x) c(media=mean(x), var=var(x), sd=sd(x), CV=100*sd(x)/mean(x)) (sim.res <- aggregate(y~gr, FUN=resumo, data=sim)) var(sim.res$y[,1]) mean(sim.res$y[,2]) mean(sim$y) ## A seguir serão obtidas inferências de três formas diferentes: ## - ajuste modelo de efeito aleatório (não bayesiano) ## - ajuste via JAGS (inferência por simulação da posteriori) ## - ajuste via INLA (inferência por aproximação da posteriori) ## ## Modelo de efeitos aleatórios ## require(lme4) fit.lme <- lmer(y ~ 1|gr, data=sim) summary(fit.lme) ranef(fit.lme) coef(fit.lme)$gr - fixef(fit.lme) print(VarCorr(fit.lme), comp="Variance") ## JAGS require(rjags) sim.lst <- as.list(sim[c("gr","y")]) sim.lst$N <- nrow(sim) sim.lst$Ngr <- length(unique(sim$gr)) mean(sim.lst$y) cat("model{ for(j in 1:N){ y[j] ~ dnorm(mu[gr[j]], tau.e) } for(i in 1:Ngr){ mu[i] ~ dnorm(theta, tau.b) } theta ~ dnorm(0, 1.0E-6) tau.b ~ dgamma(0.001, 0.001) sigma2.b <- 1/tau.b tau.e ~ dgamma(0.001, 0.001) sigma2.e <- 1/tau.e cci <- sigma2.e/(sigma2.e+sigma2.b) }", file="sim.jags") sim.jags <- jags.model(file="sim.jags", data=sim.lst, n.chains=3, n.adapt=1000) ## inits = ... fit.jags <- coda.samples(sim.jags, c("theta", "sigma2.b", "sigma2.e", "cci"), 10000, thin=10) summary(fit.jags) plot(fit.jags) ## require(INLA) fit.inla <- inla(y ~ f(gr) , family="gaussian", data=sim) summary(fit.inla) sqrt(1/fit.inla$summary.hyperpar[,1])
Atividades propostas:
- Complementar as análise acima com exploração dos resultados, obtenção de gráficos e resultados de interesse
- Ajustar o modelo acima aos dados de:
Julio M. Singer, Carmen Diva Saldiva de André, Clóvis de Araújo Peres
Confiabilidade e Precisão na Estimação de Médias
Revista Brasileira de Estatística, v73, n. 236, jan./jun. 2012. - Identificar e ajustar modelos (não bayesianos, bayesianos por simulação ou aproximados) para dados simulados da seguinte forma:
set.seed(123456L) n <- 50 m <- 10 w <- rnorm(n, sd=1/3) u <- rnorm(m, sd=1/4) b0 <- 0 b1 <- 1 idx <- sample(1:m, n, replace=TRUE) y <- rpois(n, lambda = exp(b0 + b1 * w + u[idx]
18/05
- Script R/JAGS para análise dos dados do Cap 8 (changepoint Poisson)
- Mais um exemplo de análise com efeitos aleatórios (serialmente) correlacionados
## ## Análise de conjunto de dados com INLA com efeitos aleatórios temporalmente correlacionados ## require(INLA) ## ## Visualização dos dados ## data(Tokyo) head(Tokyo) plot(y ~ time, data=Tokyo) ## colocando na forma de proporção de dias com chuva plot(y/2 ~ time, data=Tokyo) ## ## 1. Modelo "Nulo": só intercepto ## estimando a probabilidade de chuva como uma constante: fit.glm <- glm(cbind(y, n-y) ~ 1, family=binomial, data=Tokyo) abline(h=exp(coef(fit.glm))/(1+exp(coef(fit.glm))), col=2, lty=3, lwd=3) ## ou então, como neste modelo todos os valores preditos são iguais bastaria fazer: abline(h=fitted(fit.glm)[1], col=2, lty=3, lwd=3) ## ## 2. Agora o mesmo modelo nulo anterior porém ajustado pelo INLA ## modelo0 = y ~ 1 fit0 <- inla(modelo0, data=Tokyo, family="binomial", Ntrials=n, control.predictor=list(compute=TRUE)) summary(fit0) fit0$summary.fitted.values with(fit0, matlines(summary.fitted.values[,c(1,3:6)], lty=c(1,2,2,2,3), col=2)) ## ## 3. Modelo com probabilidades variando no tempo ## através da inclusão de variável/processo latente ## modelando o logito(probabilidade) como um efeito aleatório correlacionado no tempo ## segundo um "random walk" cíclico de ordem 2 modelo = y ~ 0 + f(time, model="rw2", cyclic=T, param=c(1, 0.0001)) fit <- inla(modelo, data=Tokyo, family="binomial", Ntrials=n, control.predictor=list(compute=TRUE)) ## names(fit) head(fit$summary.fitted.values) ## sobrepondo ao gráfico dos dados (moda, mediana e média são praticamente indistinguíveis) with(fit, matlines(summary.fitted.values[,c(1,3:6)], lty=c(1,2,2,2,3), col=1)) ## ## 4. Modelando usando GAM (generalised additive model) ## require(mgcv) fit.gam <- gam(cbind(y, n-y) ~ s(time), family=binomial, data=Tokyo) names(fit.gam) fitted(fit.gam, se=T) pred.gam <- predict(fit.gam, type="response", se=T, newdata=Tokyo["time"]) names(pred.gam) with(pred.gam, matlines(cbind(fit, fit+2*se.fit, fit-2*se.fit), lty=c(1,2,2), col=4))
01/06
- INLA
- Artigo recente de revisão do INLA pelos seus desenvolvedores