Essa é uma revisão anterior do documento!
Tabela de conteúdos
Variáveis Aleatórias Contínuas
Introdução
Discutiremos agora a caracterização de variáveis cujos possíveis valores ocorrem aleatoriamente e pertencem a um intervalo dos números reais: variáveis aleatórias contínuas.
Exemplos de variáveis aleatórias contínuas:
- Renda;
- Salário;
- Tempo de uso de um equipamento;
- comprimento de uma peça;
- Área atingida por certa praga agrícola.
Precisamos caracterizar a distribuição de probabilidade de uma variável aleatória contínua.
Exemplo 6.1: Estudos anteriores revelam a existência de um grande lençol de água no subsolo de uma região. No entanto, sua profundidade ainda não foi determinada, sabendo-se apenas que o lençol pode estar situado em qualquer ponto entre 20 e 100 metros.
Vamos supor que escolhemos, ao acaso, um ponto nessa região e dispomos de uma sonda que, ao fazer a perfuração, detecta com precisão a profundidade do reservatório de água.
Denotamos por X a variável aleatória representando a profundidade.
Note que apesar de X poder ser qualquer número entre 20 e 100 metros, o instrumento com que trabalhamos, pode não ser tão preciso como gostaríamos. Por exemplo, uma profundidade de 32,571 metros poderia ser medida por 32,6 metros. Vamos assumir, entretanto, que temos um instrumento ideal que não faz aproximações.
Nessas condições, podemos supor a sonda acoplada a um instrumento indicador da profundidade e um dispositivo que, quando a sonda encontrar a água, provoque a imediata interrupção da perfuração.
Uma vez que não temos informações adicionais a respeito da profundidade do lençol, é razoável assumirmos que a sonda pode parar em qualquer ponto entre 20 e 100 metros, sem que tenhamos motivos para privilegiar essa ou aquela profundidade.
- Assim, consideraremos todos os pontos como igualmente prováveis.
- Se utilizarmos a mesma idéia de atribuir a cada possível ponto uma probabilidade, teremos uma dificuldade extra, pois eles pertencem ao intervalo [20, 100], em que existem infinitos números reais.
- Se cada um deles tiver, individualmente, probabilidade maior que zero, a soma das probabilidades será igual a infinito e não 1, como requer a definição de função de probabilidade.
Em geral, em situações como esta, não é de interesse considerar um único valor para avariável aleatória, mas intervalos de valores na atribuição de probabilidades.
Neste caso, sabemos que o espaço amostral corresponde ao intervalo [20, 100] e as profundidades são igualmente prováveis.
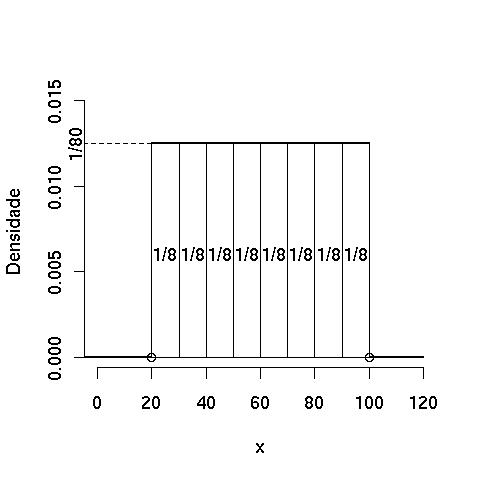
- Suponha, por um momento, que dividimos o espaço amostral em 8 intervalos de comprimento 10 ([20,30), [30,40), …, [90, 100)).
- É razoável atribuir aos intervalos a probabilidade 1/8, correspondendo à relação entre o comprimento de cada um deles e o comprimento do espaço amostral, ie, 10 para 80 ou 1/8.
Para construir um histograma podemos supor que 1/8 é a frequência relativa da ocorrência de cada um dos intervalos.
As ordenadas do gráfico são as densidades, calculadas de modo que a área de cada retângulo seja a frequência relativa (probabilidade) do intervalo.
Note que, dada as características do problema, a divisão em 8 intervalos produziu o mesmo valor de densidade de 1/80 para todos eles.
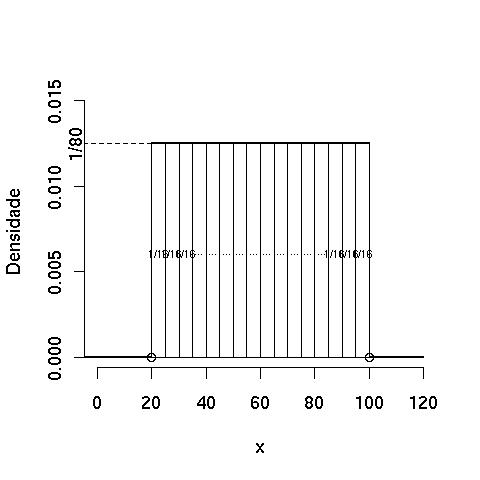
- Se dividirmos o intervalo [20, 100] em 16 faixas iguais, utilizando o mesmo argumento anterior, temos que os intervalos [20,25), [25,30), …, [95,100) terão todos a mesma probabilidade 1/16.
O histograma mostra que, apesar de termos diferentes intervalos, a densidade permanece com o mesmo valor, igual a 1/80.
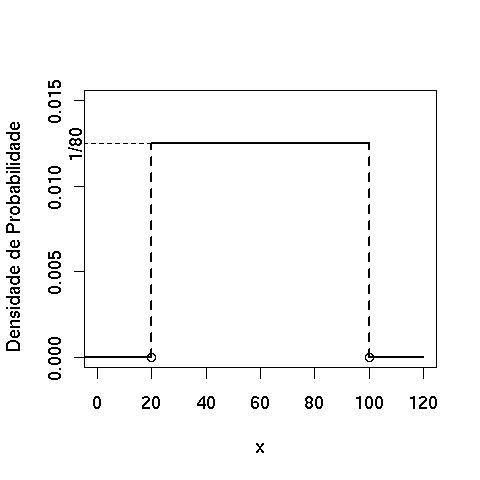
- Podemos continuar este procedimento, aumentando cada vez mais o número de faixas, com a consequente diminuição das suas amplitudes de tal forma que, em uma situação teórica com infinitos intervalos, temos o seguinte histograma:
- Agora podemos caracterizar completamente a atribuição de probabilidades para o caso contínuo. Ela será definida pela área abaixo de uma função positiva, denominada densidade de probabilidade.
- Observe que a densidade em si não é uma probabilidade, mas uma função matemática que nos auxilia na atribuição de probabilidades.
- Assim, para a variável aleatória contínua X representando a profundidade do lençol de água, a função densidade f é dada por
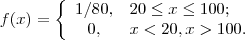
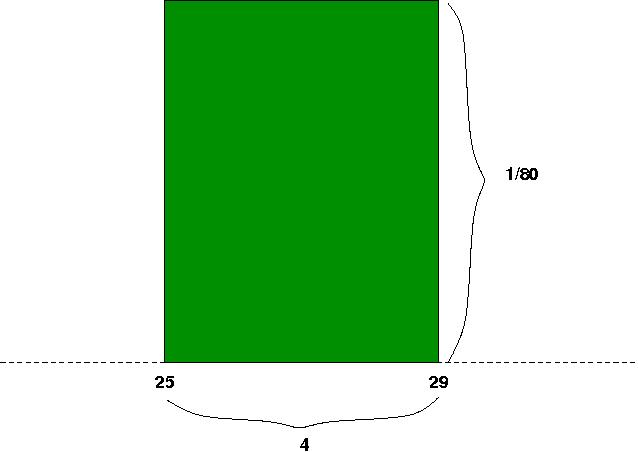
Nesse exemplo, a função densidade é bastante simples, e portanto a probabilidade de que a profundidade do lençol esteja em um dado intervalo pode ser calculada com o uso de áreas de figuras planas.
Para obter a probabilidade de uma profundidade pelo menos igual a 25, mas inferior a 29, calculamos a área do retângulo:
e, portanto, 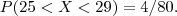
Função Densidade de Probabilidade
Dizemos que f(x) é uma função contínua de probabilidade ou função densidade de probabilidade para uma variável aleatória contínua X, se satisfaz duas condições:
- f(x) ≥ 0, para todo
 ;
; - A área definida por f(x) é igual a 1, ou seja,
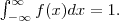
Da mesma forma, para calcular probabilidades, temos que para 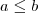 .
.
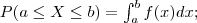
a integral acima, indica a área sob a função f definida pelo intervalo [a,b].
- OBS: Teremos área zero sob qualquer valor individual, ie, P(X=k)=0 para qualquer k. Portanto, em se tratando de variáveis aleatórias contínuas, a probabilidade de ocorrência de um valor isolado é sempre zero e consequentemente, as probabilidades calculadas sobre os intervalos [a,b], [a,b), (a,b] e (a,b) são as mesmas, para quaisquer valores de a e b.
Exemplo 6.2: Arqueólogos estudaram uma certa região e estabeleceram um modelo teórico para a variável C, comprimento de fósseis da região (em cm). Suponha que C é uma variável aleatória contínua coma a seguinte função densidade de probabilidade:
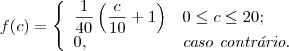
É direto verificar que :
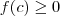
e calculando a área abaixo da função (representa o cálcula da área de um trapézio) verifica-se que esta é igual a 1. Portanto, 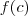 é uma função de densidade de probabilidade.
é uma função de densidade de probabilidade.
A probabilidade de escolher ao acaso um fóssil e este apresentar comprimento inferior a 8 cm, pode ser calculada através da área de um trapézio com altura menor.
Como exercício, construa o gráfico da função 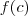 no intervalo de 0 a 20 e verifique que a área requerida, ou seja,
no intervalo de 0 a 20 e verifique que a área requerida, ou seja,
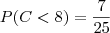 .
.
Medidas de posição para variáveis aleatórias contínuas
Definição: Valor esperado também conhecido por média, expectância ou esperança de uma variável aleatória contínua X é dado pela expressão :
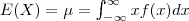
A expressão apresentada acima assemelha-se à utilizada para variáveis aleatórias discretas, substituindo o símbolo de somatório pelo símbolo de integral.
Definição: A mediana de uma variável aleatória contínua é um valor Md que satisfaz a seguinte propriedade :
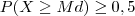 e
e
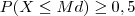
Definição A moda de uma variável aleatória X é o valor Mo tal que:
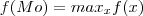
ou seja, Mo é o valor de máximo da função f(x).
Variância de uma variável aleatória contínua
Para uma variável aleatória X com densidade f(x), a variância é dada por:
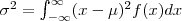
alternativamente, ela pode ser calculada por:
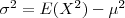
onde
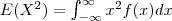 .
.
O desvio padrão  é calculado através da raiz da variância.
é calculado através da raiz da variância.
Principais Modelos Contínuos
O modelo probabilístico para uma variável aleatória contínua é especificado através da forma funcional de f(x), a função densidade de probabilidade que deve ser positiva e com integral igual a 1. Serão vistos 3 dos principais modelos conínuos: uniforme, exponencial e normal.
Modelo Uniforme Contínuo
O primeiro modelo a ser apresentado traz uma situação análoga ao modelo uniforme discreto. Uma variável que assume valores no intervalo [a,b] com a<b , é dita ter distribuição uniforme contínua se sua função densidade de probabilidade é dada por :
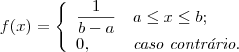
Neste caso, a função f(x) é constante no intervalo [a,b] e sua área total pode ser calculada através da área de um retângulo de base b-a e altura 1/(b-a). Pelo produto da base pela altura do retângulo, verificamos que esta é uma função densidade de probabilidade pois sua área é igual a 1.
No modelo uniforme contínuo, a média e variância são dados respectivamente por :
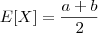
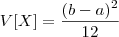
Como as probabilidades estão simetricamente distribuídas em torno da média, esta será igual a mediana no modelo uniforme.
Modelo Exponencial
O modelo exponencial é muito aplicado quando o interesse é descrever em termos probabilísticos o tempo (espaço) até a ocorrência de um evento de interesse. Alguns exemplos de variáveis modeladas por esta distribuição são :
- Tempo de espera na linha telefônica até o serviço de atendimento
- Tempo até a ativação de um neurônio
- Tempo de vida de um paciente com câncer
- Distância até encontrar uma deformidade em uma rodovia.
De forma mais geral, uma variável aleatória contínua é modelada pela distribuição exponencial se sua função densidade de probabilidade é descrita por:
f(x)= α eαx</sup>, x≥0.
Para o modelo exponencial, a média e variância são inversamente proporcionais ao parâmetro α:
E[X]=1/α e V[X] = 1/α².
Na distribuição exponencial, a probabilidade da variável aleatória pertencer ao intervalo (a,b) é obtida através de :
P(a ≤ X ≤ b)= ∫αexp(αx) dx= exp(α a)-exp(α b)
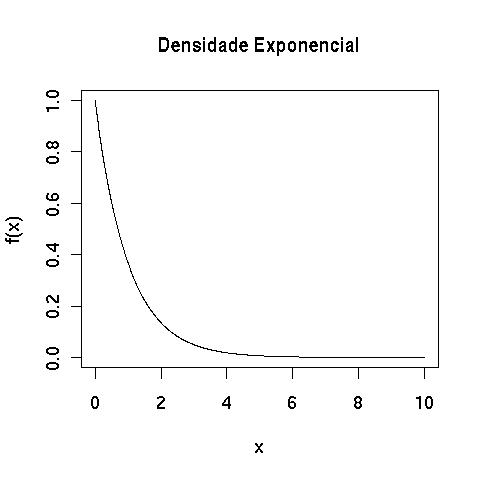 Exemplo 6.3 Uma indústria fabrica lâmpadas especiais que ficam em operação continuamente. A empresa oferece a seus clientes a garantia de reposição caso a lâmpada dure menos de 50 horas. A vida útil desta lâmpada é modelada pela distribuição exponencial com parâmetro 1/8000. Qual a proporção de lâmpadas trocadas por defeito ?
Neste exemplo,
<latex>\alpha=\dfrac{1}{8000}</latex>
e a proporção a ser calculada é representada pela probabilidade :
<latex> P(0 \leq X \leq 50)=e^{
Exemplo 6.3 Uma indústria fabrica lâmpadas especiais que ficam em operação continuamente. A empresa oferece a seus clientes a garantia de reposição caso a lâmpada dure menos de 50 horas. A vida útil desta lâmpada é modelada pela distribuição exponencial com parâmetro 1/8000. Qual a proporção de lâmpadas trocadas por defeito ?
Neste exemplo,
<latex>\alpha=\dfrac{1}{8000}</latex>
e a proporção a ser calculada é representada pela probabilidade :
<latex> P(0 \leq X \leq 50)=e^{\frac{0}{8000}}-e^{\frac{50}{8000}}=0,006</latex>
e desta forma, espera-se que apenas 0,6% das lâmpadas fabricadas sejam trocadas por defeito. Repare que esta pequena probabilidade representa uma informação consistente com o tempo médio de vida útil da lâmpada que é igual a 8000 horas, ou seja, o inverso do parâmetro da distribuição exponencial.
Comentário 1: a distribuição exponencial está diretamente ligada à distribuição Poisson, inclusive o parâmetro <latex>\alpha</latex> representa a intensidade de ocorrência do evento de interesse em uma unidade de tempo/espaço.
Comentário 2: a distribuição exponencial possui uma propriedade chamada "falta de memória" (no inglês memoryless). Esta propriedade é expressa pela igualdade abaixo:
<latex>
P(X > t+s|X>s)=P(X>t)
</latex>
==== Modelo Normal (Gaussiano) ====
O modelo normal, ou Gaussiano, é certamente o mais importante dos modelos para variáveis aleatórias contínuas. Isto justifica-se pelo grande número de aplicações que a utilizam e pela sua capacidade de aproximar outros modelos.
A função de densidade de probabilidade da distribuição normal é dada por:
<latex>
f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{\frac{(x\mu)^2}{2\sigma^2} } ~~~\text{para} \infty < x < \infty
</latex>
Algumas importantes propriedades desta distribuição são :
- <latex>f(x\mu)=f(\mu-x)</latex>
- <latex> \lim_{x\rightarrow \infty}f(x)=\lim_{x\rightarrow \infty}f(x)=0 </latex>
- <latex> arg\max_{x} f(x) = \mu </latex>
Nesta distribuição, a média, mediana e moda são valores coincidentes.
\dfrac{(x-\mu)^2}{2\sigma^2}}
</latex>
recorremos à métodos numéricos e os resultados obtidos são aproximados.
== Normal padronizada ==
Para auxiliar o cálculo de probabilidades para uma variável X, através da distribuição normal, foi desenvolvida uma tabela para uma variável padronizada, que chamamos aqui de Z.
<latex>
Z=\dfrac{X-\mu}{\sigma}
</latex>
Z representa a quantidade de desvios-padrão que X dista da média.
Exemplo 6.4 Em uma sala de aula, os alunos apresentam, em média (<latex>\mu</latex>) 8 anos de idade com um desvio padrão (<latex>\sigma</latex>) igual a 2,5 anos. Para um grupo de 5 alunos, associou-se a cada um deles a sua idade padronizada, conforme a expressão acima.
<latex>
\begin{tabular}{c|ccccc}
Aluno & 1 & 2 & 3 & 4 & 5 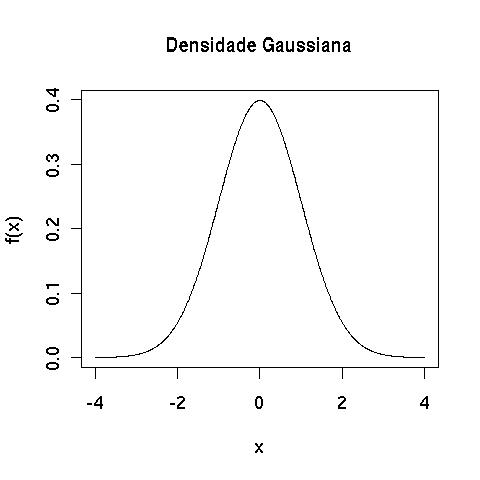 O cálculo de probabilidades na distribuição normal é feito mediante o conhecimento da média e desvio-padrão da variável aleatória. Dada a importância desta distribuição, estas duas medidas são consideradas as mais importantes para verificar tendência central e dispersão, respectivamente.
Embora a média e o desvio-padrão sejam os parâmetros para o cálculo de probabilidades na distribuição normal, para avaliar a expressão:
<latex>
P(a\leq X \leq b)= \displaystyle\int_{a}^b \dfrac{1}{\sqrt{2\pi}}e^{
O cálculo de probabilidades na distribuição normal é feito mediante o conhecimento da média e desvio-padrão da variável aleatória. Dada a importância desta distribuição, estas duas medidas são consideradas as mais importantes para verificar tendência central e dispersão, respectivamente.
Embora a média e o desvio-padrão sejam os parâmetros para o cálculo de probabilidades na distribuição normal, para avaliar a expressão:
<latex>
P(a\leq X \leq b)= \displaystyle\int_{a}^b \dfrac{1}{\sqrt{2\pi}}e^{
\hline
Idade (X) & 7 & 5 & 8 & 4 & 6
Idade Padr. (Z) &- 0,4 & 1,2 & 0 & -1,6 & -0,8 \mu}{\sigma}\leq Z \leq \dfrac{b-\mu}{\sigma}\right)</latex>
Exemplo 6.5: Um estudo foi realizado para medir o nível de estresse de alunos durante o exame de matemática. Foi Constatado que o nível de estresse apresenta distribuição normal com média igual a 8,2 e desvio-padrão igual a 1,34. Em um próximo exame, qual a probabilidade de um determinado aluno ter estresse com nível entre 9 e 10?
\end{tabular}
</latex>
Ao utilizar o escore padronizado, dizemos que o aluno 4, por exemplo, está 1,6 desvios-padrão abaixo da média. De fato, com exceção do aluno 3, todos os outros alunos estão abaixo da média de idade da turma, <latex>\mu=8</latex>.
Repare que para uma variável padronizada, as probabilidades podem ser obtidas :
<latex>P(a\leq X \leq b)=P\left(\dfrac{a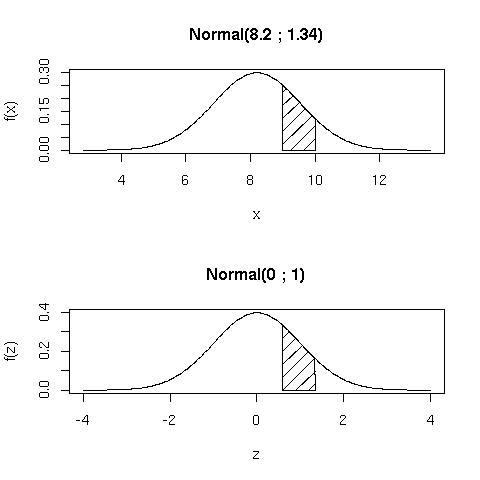 A probabilidade questionada é encontrada através da área hachurada sob a curva normal exibida na figura acima. As áreas da normal comum e da normal padronizada são equivalentes. Portanto, com auxílio de uma tabela chega-se ao resultado:
<latex>
P(9<X<10)=
</latex>
<latex>
P\left(\dfrac{9-8,2}{1,34}<Z<\dfrac{10-8,2}{1,34}\right)=
</latex>
<latex>
P(0,597<Z<1,343)=0,186
</latex>
O resultado indica que 18,6% dos estudantes têm nível de estresse entre 9 e 10. Esta probabilidade pode ser encontrada com auxílio de tabelas que em geral acompanham livros de estatística básica como a primeira encontrada neste link de tabelas.
==== Aproximação da Distribuição Binomial pela Normal ====
Em algumas situações, o cálculo de probabilidades de uma variável pode ser feito de modo aproximado utilizando a distribuição normal, mesmo que esta variável possua uma outra distribuição. Não serão todas as distribuições "não-normais" que se encaixarão nestes casos, mas algumas como a binomial são razoavelmente aproximadas pela normal sob algumas condições.
Vejamos o seguinte exemplo em Magalhães e Lima (2004).
Exemplo 6.6: Estudo do sindicato dos bancários indica que cerca de 30% dos funcionários de um banco têm problemas de estresse, provenientes das condições de trabalho. Numa amostra de 200 bancários, qual seria a probabilidade de pelo menos 50 com essa doença ?
Pela descrição da variável em questão,
<latex>X:\textit{número de bancários com estresse em 200}</latex>
o modelo binomial é adequado para calcular as probabilidades,
<latex>X\sim\textit{binomial}(200 ; 0,3) </latex>
que serão obtidas a partir de:
<latex> P(X \geq 50)=\sum_{k=50}^{200}\binom{200}{ k}0,3^x 0,7^{200-k}=0,9484</latex>.
Entretanto, este cálculo somente é viável se for utilizado um computador ou uma calculadora já programada para efetuar tal operação, pois envolve a somatória de 151 probabilidades. Uma das formas de obter este resultado, de modo aproximado, é admitir que X é uma variável aleatória contínua e, pelas próprias características da distribuição binomial, a normal torna-se candidata natural para reger as probabilidades nesta aproximação. Então, com esta aproximação :
se
<latex>
X\sim \textit{binomial}(n,p)
</latex>
então,
<latex>
X \approx \textit{Normal}(np,\sqrt{np(1-p)})
</latex>
No exemplo acima, os parâmetros da distribuição normal corresponderiam à média e desvio padrão da binomial, obtidos respectivamente por :
<latex>np=60~~ e ~~\sqrt{np(1-p)}=\sqrt{42}</latex>.
Denominando Y uma variável com distribuição normal, conforme os parâmetros acima, calculamos a probabilidade requisitada com o uso da distribuição aproximada:
<latex>
P(X\geq50) \approx P\left(\dfrac{Y-60}{\sqrt{42}} \geq \dfrac{50-60}{\sqrt{42}}\right)=P(Z\geq-1,54)=0,9382
</latex>
Em valor absoluto, a diferença da aproximação foi igual a |0,9382-0,9484|=0,0102. Notamos que o erro de aproximação subestima a probabilidade verdadeira em um pouco mais de 1%. Em algumas situações, especialmente àquelas onde n é pequeno, este erro pode ser mais dramático. Um procedimento utilizado para melhorar a aproximação é utilizar a chamada correção de continuidade.
Para uma variável aleatória discreta, faz sentido calcular a probabilidade P(X=k), entretanto ao aproximá-la por uma variável aleatória contínua, tal probabilidade resultaria em zero. Para garantir, de modo aproximado, que seja encontrado o valor desta probabilidade uma saída é aplicar a correção de continuidade de modo que para a variável aleatória contínua Y tenhamos, por exemplo:
<latex>
P(X=k)\approx P(k-0,5 \leq Y \leq k+0,5)
</latex>
que representa uma probabilidade aproximada da variável aleatória discreta X assumir o valor k. Em nosso caso, Y segue a distribuição normal.
A correção de continuidade no Exemplo 6.6 é feita de modo a garantir a inclusão do valor 50 para o cálculo da probabilidade, desta forma :
<latex>
P(X\geq50) \approx P(Y>49,5)=
</latex>
<latex>
P\left(\dfrac{Y-60}{\sqrt{42}} \geq \dfrac{49,5-60}{\sqrt{42}}\right)=P(Z\geq-1,6202)=0,9474
</latex>
e com a correção, o erro absoluto da aproximação passa a ser |0,9474-0,9484|=0,001.
==== Propriedades da Distribuição Normal ====
Algumas propriedades tornam ainda mais importante o uso da distribuição normal na teoria de inferência estatística que será vista nos próximos capítulos. Uma das principais propriedades será enunciada e não demonstrada.
* A combinação linear de variáveis aleatórias independentes e normais gera uma variável aleatória com distribuição normal.
Seja <latex>X_1,X_2,\ldots,X_n </latex> uma sequência de variáveis aleatórias independentes, normalmente distribuídas com média <latex> \mu_i</latex> e variância <latex>\sigma_i^2</latex>, uma combinação linear:
<latex>
W=\sum_{i=1}^n a_i X_i
</latex>
onde
<latex>a_1,a_2,\ldots,a_n</latex> são constantes quaisquer,
segue a distribuição normal com média e variância dados respectivamente por:
<latex>
E(W)=E \left( \sum_{i=1}^n a_i X_i \right) = \sum_{i=1}^n a_i \mu_i
</latex>
<latex>
Var(W)=Var \left( \sum_{i=1}^n a_i X_i \right) = \sum_{i=1}^n a_i^2 \sigma_i^2
</latex>
O resultado faz com que a distribuição normal possa ser utilizada em várias situações . Veja o exemplo abaixo retirado de Magalhães e Lima (2004).
Exemplo 6.7 Uma corretora negocia títulos na Bolsa de Valores e utiliza um modelo probabilístico para avaliar seus lucros. Suas aplicações financeiras de compra e venda atingem três áreas: agricultura, indústria e comércio. Admita que o seguinte modelo representa o comportamento do lucro diário da corretora (em milhões de reais)
:
<latex>
L=2L_A+5L_I+3L_C,
</latex>
com LA,LI, e LC representando, respectivamente, os lucros diários nos setores de agricultura, indústria e comércio. As distribuições de probabilidade dessas variáveis aleatórias são :
<latex>L_A \sim \textit{Normal}(3,4)</latex>
<latex>L_I \sim \textit{Normal}(6,9)</latex>
<latex>L_C \sim \textit{Normal}(4,16)</latex>.
Supondo independência entre os três setores, qual será a probabilidade de um lucro diário acima de 50 mil ?
Para responder a pergunta acima, iremos utilizar a propriedade da distribuição normal que assegura que a combinação linear de normais independentes também será explicada por um modelo normal. Desta forma, o lucro <latex>L</latex> segue distribuição normal com média e variância dados respectivamente por :
<latex>\mu_L=2\mu_{L_A}+5\mu_{L_I}+3\mu_{L_C}=48</latex>
<latex>\sigma_L^2=4\sigma_{L_A}^2+25\sigma_{L_I}^2+9\sigma_{L_C}^2=385</latex>
A probabilidade do lucro diário a corretora ser maior do que 50 é obtido através de:
<latex>P(L>50)=P\left( Z>\dfrac{50-48}{\sqrt{385}}\right) =P(Z>0,10)=0,4602</latex>
com este resultado, espera-se que em 46% dos dias de operação, a corretora tenha lucro diário acima de 50 mil.
A probabilidade questionada é encontrada através da área hachurada sob a curva normal exibida na figura acima. As áreas da normal comum e da normal padronizada são equivalentes. Portanto, com auxílio de uma tabela chega-se ao resultado:
<latex>
P(9<X<10)=
</latex>
<latex>
P\left(\dfrac{9-8,2}{1,34}<Z<\dfrac{10-8,2}{1,34}\right)=
</latex>
<latex>
P(0,597<Z<1,343)=0,186
</latex>
O resultado indica que 18,6% dos estudantes têm nível de estresse entre 9 e 10. Esta probabilidade pode ser encontrada com auxílio de tabelas que em geral acompanham livros de estatística básica como a primeira encontrada neste link de tabelas.
==== Aproximação da Distribuição Binomial pela Normal ====
Em algumas situações, o cálculo de probabilidades de uma variável pode ser feito de modo aproximado utilizando a distribuição normal, mesmo que esta variável possua uma outra distribuição. Não serão todas as distribuições "não-normais" que se encaixarão nestes casos, mas algumas como a binomial são razoavelmente aproximadas pela normal sob algumas condições.
Vejamos o seguinte exemplo em Magalhães e Lima (2004).
Exemplo 6.6: Estudo do sindicato dos bancários indica que cerca de 30% dos funcionários de um banco têm problemas de estresse, provenientes das condições de trabalho. Numa amostra de 200 bancários, qual seria a probabilidade de pelo menos 50 com essa doença ?
Pela descrição da variável em questão,
<latex>X:\textit{número de bancários com estresse em 200}</latex>
o modelo binomial é adequado para calcular as probabilidades,
<latex>X\sim\textit{binomial}(200 ; 0,3) </latex>
que serão obtidas a partir de:
<latex> P(X \geq 50)=\sum_{k=50}^{200}\binom{200}{ k}0,3^x 0,7^{200-k}=0,9484</latex>.
Entretanto, este cálculo somente é viável se for utilizado um computador ou uma calculadora já programada para efetuar tal operação, pois envolve a somatória de 151 probabilidades. Uma das formas de obter este resultado, de modo aproximado, é admitir que X é uma variável aleatória contínua e, pelas próprias características da distribuição binomial, a normal torna-se candidata natural para reger as probabilidades nesta aproximação. Então, com esta aproximação :
se
<latex>
X\sim \textit{binomial}(n,p)
</latex>
então,
<latex>
X \approx \textit{Normal}(np,\sqrt{np(1-p)})
</latex>
No exemplo acima, os parâmetros da distribuição normal corresponderiam à média e desvio padrão da binomial, obtidos respectivamente por :
<latex>np=60~~ e ~~\sqrt{np(1-p)}=\sqrt{42}</latex>.
Denominando Y uma variável com distribuição normal, conforme os parâmetros acima, calculamos a probabilidade requisitada com o uso da distribuição aproximada:
<latex>
P(X\geq50) \approx P\left(\dfrac{Y-60}{\sqrt{42}} \geq \dfrac{50-60}{\sqrt{42}}\right)=P(Z\geq-1,54)=0,9382
</latex>
Em valor absoluto, a diferença da aproximação foi igual a |0,9382-0,9484|=0,0102. Notamos que o erro de aproximação subestima a probabilidade verdadeira em um pouco mais de 1%. Em algumas situações, especialmente àquelas onde n é pequeno, este erro pode ser mais dramático. Um procedimento utilizado para melhorar a aproximação é utilizar a chamada correção de continuidade.
Para uma variável aleatória discreta, faz sentido calcular a probabilidade P(X=k), entretanto ao aproximá-la por uma variável aleatória contínua, tal probabilidade resultaria em zero. Para garantir, de modo aproximado, que seja encontrado o valor desta probabilidade uma saída é aplicar a correção de continuidade de modo que para a variável aleatória contínua Y tenhamos, por exemplo:
<latex>
P(X=k)\approx P(k-0,5 \leq Y \leq k+0,5)
</latex>
que representa uma probabilidade aproximada da variável aleatória discreta X assumir o valor k. Em nosso caso, Y segue a distribuição normal.
A correção de continuidade no Exemplo 6.6 é feita de modo a garantir a inclusão do valor 50 para o cálculo da probabilidade, desta forma :
<latex>
P(X\geq50) \approx P(Y>49,5)=
</latex>
<latex>
P\left(\dfrac{Y-60}{\sqrt{42}} \geq \dfrac{49,5-60}{\sqrt{42}}\right)=P(Z\geq-1,6202)=0,9474
</latex>
e com a correção, o erro absoluto da aproximação passa a ser |0,9474-0,9484|=0,001.
==== Propriedades da Distribuição Normal ====
Algumas propriedades tornam ainda mais importante o uso da distribuição normal na teoria de inferência estatística que será vista nos próximos capítulos. Uma das principais propriedades será enunciada e não demonstrada.
* A combinação linear de variáveis aleatórias independentes e normais gera uma variável aleatória com distribuição normal.
Seja <latex>X_1,X_2,\ldots,X_n </latex> uma sequência de variáveis aleatórias independentes, normalmente distribuídas com média <latex> \mu_i</latex> e variância <latex>\sigma_i^2</latex>, uma combinação linear:
<latex>
W=\sum_{i=1}^n a_i X_i
</latex>
onde
<latex>a_1,a_2,\ldots,a_n</latex> são constantes quaisquer,
segue a distribuição normal com média e variância dados respectivamente por:
<latex>
E(W)=E \left( \sum_{i=1}^n a_i X_i \right) = \sum_{i=1}^n a_i \mu_i
</latex>
<latex>
Var(W)=Var \left( \sum_{i=1}^n a_i X_i \right) = \sum_{i=1}^n a_i^2 \sigma_i^2
</latex>
O resultado faz com que a distribuição normal possa ser utilizada em várias situações . Veja o exemplo abaixo retirado de Magalhães e Lima (2004).
Exemplo 6.7 Uma corretora negocia títulos na Bolsa de Valores e utiliza um modelo probabilístico para avaliar seus lucros. Suas aplicações financeiras de compra e venda atingem três áreas: agricultura, indústria e comércio. Admita que o seguinte modelo representa o comportamento do lucro diário da corretora (em milhões de reais)
:
<latex>
L=2L_A+5L_I+3L_C,
</latex>
com LA,LI, e LC representando, respectivamente, os lucros diários nos setores de agricultura, indústria e comércio. As distribuições de probabilidade dessas variáveis aleatórias são :
<latex>L_A \sim \textit{Normal}(3,4)</latex>
<latex>L_I \sim \textit{Normal}(6,9)</latex>
<latex>L_C \sim \textit{Normal}(4,16)</latex>.
Supondo independência entre os três setores, qual será a probabilidade de um lucro diário acima de 50 mil ?
Para responder a pergunta acima, iremos utilizar a propriedade da distribuição normal que assegura que a combinação linear de normais independentes também será explicada por um modelo normal. Desta forma, o lucro <latex>L</latex> segue distribuição normal com média e variância dados respectivamente por :
<latex>\mu_L=2\mu_{L_A}+5\mu_{L_I}+3\mu_{L_C}=48</latex>
<latex>\sigma_L^2=4\sigma_{L_A}^2+25\sigma_{L_I}^2+9\sigma_{L_C}^2=385</latex>
A probabilidade do lucro diário a corretora ser maior do que 50 é obtido através de:
<latex>P(L>50)=P\left( Z>\dfrac{50-48}{\sqrt{385}}\right) =P(Z>0,10)=0,4602</latex>
com este resultado, espera-se que em 46% dos dias de operação, a corretora tenha lucro diário acima de 50 mil.