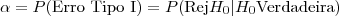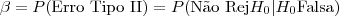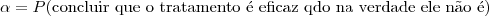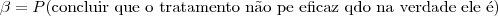Tabela de conteúdos
Introdução
Em geral, intervalos de confiança são a forma mais informativa de apresentar os achados pricipais de um estudo.
Contudo, algumas vezes existe um particular interesse em decidir sobre a verdade ou não de uma hipótese específica (se dois grupos têm a mesma média ou não, ou se o parâmetro populacional tem um valor em particular ou não).
Os testes de hipóteses fornecem-nos uma estrutura para que façamos isto.
Teste para a Média Populacional
Vamos desenvolver as idéias gerais de teste de hipótese supondo, inicialmente, que o modelo Normal é adequado para os dados.
Veja o exemplo a seguir retirado de Magalhães e Lima (2004):
Exemplo 8.1: Suponha que, entre pessoas sadias, a concentração de certa substância no sangue se comporta segundo um modelo Normal com média 14 unidades/ml e desvio padrão 6 unidades/ml. Pessoas sofrendo de uma doença específica têm a concentração média da substância alterada para 18 unidades/ml. Admitimos que o modelo Normal, com desvio padrão 6 unidades/ml continua representando de forma adequada a concentração da substância em pessoas com a doença.
Desejamos averiguar se um certo tratamento, proposto para combater a doença é eficaz. Uma amostra aleatória de tamanho n=30 é selecionada entre indivíduos doentes que foram submetidos ao tratamento. Sabemos que para i=1,2,…,30, temos Xi~N(μ,36), sendo μ=14 ou μ=18 dependendo do tratamento ser eficiente ou não.
Caso a amostra de 30 valores forneça valor médio de concentração alto e "próximo" de 18, teremos evidências de que o tratamento não é eficaz, ao passo que um valor baixo e "próximo" de 14 unidades/ml nos revelaria crer que o tratamento apresenta resultados satisfatórios. Isto é, se o tratamento for eficaz, então os 30 indivíduos podem ser vistos como membros da população com concentração modelada por uma N(14,36), caso contrário, eles pertencerão à população N(18,36).
No exemplo acima, o interesse consiste em testar se a média populacional μ é igual a 14, caso em que os indivíduos pertencem à população de sadios, contra a alternativa de ser igual a 18, valor que corresponde à população de doentes.
Como estamos tratando com a média populacional, utilizaremos, no teste a média amostral 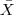 , um estimador não-viciado e consistente de μ. Será baseado no valor observado de
, um estimador não-viciado e consistente de μ. Será baseado no valor observado de 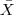 , denotado por
, denotado por 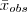 , que tomaremos nossa decisão a respeito da eficácia da tratamento proposto.
, que tomaremos nossa decisão a respeito da eficácia da tratamento proposto.
Pelas suposições feitas acima, a concentração da substância segue um modelo Normal com desvio padrão de 6 unidades/ml. Então, para o tamanho de amostra igual a 30, a média amostral terá distribuição N(μ,36/30).
Um critério que pode ser utilizado, para decidir sobre o valor de μ, é determinar um valor crítico, digamos 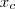 , tal que se
, tal que se 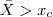 , concluímos que a amostra pertence à população com média μ=18, ou seja, o tratamento não é eficaz.
, concluímos que a amostra pertence à população com média μ=18, ou seja, o tratamento não é eficaz.
Por outro lado, quando 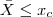 , concluímos que a amostra pertence à população com média μ=14, sendo o tratamento considerado eficaz.
, concluímos que a amostra pertence à população com média μ=14, sendo o tratamento considerado eficaz.
Erros de Decisão
É importante ter em mente que, para a argumentação anterior ficar completa, precisamos determinar o valor 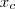 e quantificar os erros associados às possíveis conclusões. Observe que, sendo
e quantificar os erros associados às possíveis conclusões. Observe que, sendo 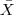 uma variável aleatória, corremos o risco de concluir incorretamente que o tratamento é eficaz. Ou, de modo recíproco, decidir que o tratamento não é eficiente quando ele é.
uma variável aleatória, corremos o risco de concluir incorretamente que o tratamento é eficaz. Ou, de modo recíproco, decidir que o tratamento não é eficiente quando ele é.
As duas hipóteses sobre a eficácia do tratamento são denotadas por H0 e Ha e, usualmente, denominadas hipótese nula e hipótese alternativa.
H0: O tratamento não é eficaz
Ha: O tratamento é eficaz
Essas hipóteses correspondem aos diferentes valores do parâmetro μ e, assim, podemos reescrevê-las como:
H0: μ=18 versus Ha: μ=14 (teste de hipóteses simples)
No caso do tratamento ser eficaz, é razoável assumirmos que ele foi capaz de fazer com que os indivíduos da amostra mudassem para uma população cuja média é inferior a 18, caso contrário, se o tratamento é ineficaz, μ não se alteraria. Assim, as hipóteses de interesse seriam escritas como
H0: μ=18 versus Ha: μ<18 (teste de hipóteses unilateral)
Para verificarmos se o tratamento produz algum efeito, seja ele benéfico (μ<18) ou danoso (μ>18), devemos construir um teste bilateral:
H0: μ=18 versus Ha: μ≠18 (teste de hipóteses bilateral)
Por conveniência técnica deixamos sempre a igualdade na hipótese nula.
Os dois erros que podem ser cometidos ao se realizar um teste de hipóteses são:
- Erro do Tipo I: Rejeitar a hipótese H0, quando H0 é verdadeira, e
- Erro do Tipo II: Não rejeitar a hipótese H0, quando H0 é falsa.
Denotamos
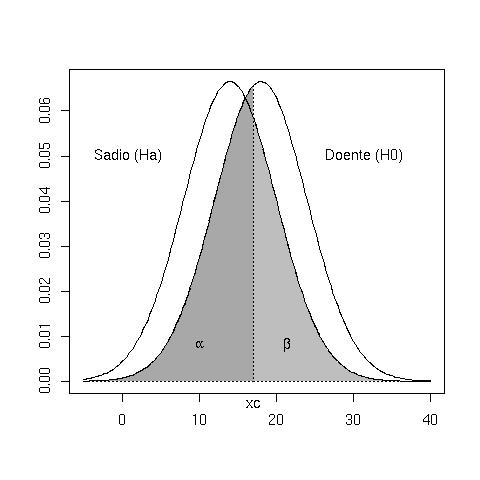
Considerando as hipóteses H0: μ=18 versus Ha: μ<18, temos a seguinte interpretação para os erros:
A situação ideal é aquela em que ambas as probabilidades, α e β, são próximas de zero. Entretanto, à medida que diminuímos α, β tende a aumentar.
Veja como dependendo do posicionamento de 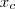 , a diminuição de α implica num aumento de β.
, a diminuição de α implica num aumento de β.
Levando isso em conta, devemos cuidar para que, ao definir as hipóteses, o erro mais importante a ser evitado seja o erro do tipo I. Á sua probabilidade α damos o nome de nível de significância do teste.
Encontrando o valor crítico
Supondo α conhecido, vamos descrever como determinar o valor crítico 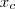 .
.
Inicialmente, note que
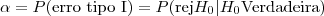
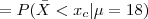
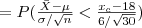
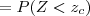
com Z~N(0,1). Portanto, dado α obtemos zc na tabela da Normal e calculamos xc da seguinte forma:
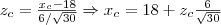
Por exemplo, para α=0,05 temos
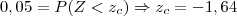
logo
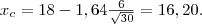
Uma vez colhida a amostra, se a estimativa  ; rejeitamos a hipótese nula concluindo que o tratamento é eficaz.
; rejeitamos a hipótese nula concluindo que o tratamento é eficaz.
A região dada pelo conjunto dos números reais menores que 16,20 é denominada de Região de Rejeição ou Região Crítica e representada por RC.
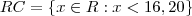
Se a amostra obtida forneceu a estimativa  ; que pertence à RC, rejeitamos H0 ao nível de significância de α=0,05.
; que pertence à RC, rejeitamos H0 ao nível de significância de α=0,05.
A construção de testes de hipóteses bilaterais é feita de maneira similar à apresentada para o caso unilateral, exceto que, agora, devemos considerar uma Região de Rejeição composta de duas partes disjuntas.
Para exemplificar, suponha que μ0 é uma constante conhecida e que as hipóteses nula e alternativa são expressas como
H0: μ=μ0 versus Ha: μ≠μ0
A Região Crítica será dada por
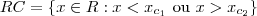
e, para um valor α fixado, determinamos os números 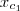 e
e 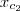 de modo que
de modo que
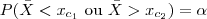
Dada a simetria da densidade Normal, distribuímos a massa α igualmente entre as duas partes da Região de Rejeição. Isto é,
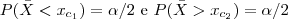
Sumário
Sumário das estapas para a realização de um teste de hipóteses:
- Estabelecer as hipóteses nula e alternativa
- Definir a forma da região crítica, com base na hipótese alternativa
- Identificar a distribuição do estimador e obter sua estimativa
- Fixar α e obter a região crítica
- Concluir o teste com base na estimativa e na região crítica
O exemplo 8.4 de Magalhães e Lima (2004) ilustra as etapas acima descritas com um teste para uma proporção.
Nos testes desenvolvidos nesta seção, duas suposições básicas foram feitas:
- a variável aleatória de interesse na população segue o modelo Normal
- a variância é conhecida
A ausência de normalidade pode ser contornada com o auxílio do Teorema Central do Limite o qual garante que, para amostras grandes, a média amostral tem distribuição Normal.
Nestes casos praticamente não haverá alteração nos procedimentos que estudamos até agora, pois continuamos a usar a densidade Normal para estabelecer a região crítica. Entretanto, se a variância for desconhecida, ela precisará ser estimada e precisaremos de uma nova distribuição para 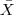 .
.
Teste para a Média com Variância Desconhecida
Inicialmente, manteremos a suposição de que a variável aleatória de interesse tem distribuição Normal.
Se o desvio-padrão é desconhecido, ele precisa ser estimado. Supondo que nossa amostra aleatória seja representada pelo vetor de variáveis aleatórias 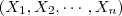 , todas elas com densidade Normal de média μ e variância σ2. Vamos utilizar o "melhor" estimador que conhecemos para σ2, a variância amostral
, todas elas com densidade Normal de média μ e variância σ2. Vamos utilizar o "melhor" estimador que conhecemos para σ2, a variância amostral 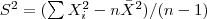 .
.
Definindo agora a variável padronizada
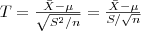
vemos que T também é uma variável aleatória. Entretanto, apesar de 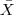 ter distribuição Normal, denominador envolve a variável aleatória
ter distribuição Normal, denominador envolve a variável aleatória 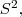 que fará com que a função densidade de T seja diferente da Normal, afinal T surge a partir da razão entre duas variáveis aleatórias
que fará com que a função densidade de T seja diferente da Normal, afinal T surge a partir da razão entre duas variáveis aleatórias 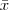 e
e 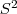 , respectivamente.
, respectivamente.
Esta nova densidade, que pode ser deduzida teoricamente, é denominada t de Student e seu parâmetro tem o nome de graus de liberdade, neste caso correspondendo ao tamanho da amostra aleatória subtraído de 1.
A medida em que o tamanho da amostra aumenta a distribuição da variável T se aproxima da distribuição de Z, a normal padronizada. Isto ocorrem em conseq\"uência das propriedades de 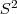 que é não viciado e consistente para
que é não viciado e consistente para 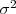 . Este resultado pode ser expresso como:
. Este resultado pode ser expresso como:
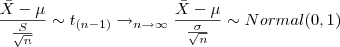
A notação utilizada será 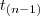 e, devido à complexidade da sua função densidade, as probabilidades são obtidas de tabelas construídas numericamente. A exemplo da Normal, o modelo t-Student tem densidade em forma de sino, entretanto, as caudas tem maior massa que a N(0,1).
e, devido à complexidade da sua função densidade, as probabilidades são obtidas de tabelas construídas numericamente. A exemplo da Normal, o modelo t-Student tem densidade em forma de sino, entretanto, as caudas tem maior massa que a N(0,1).
*Exemplo 8.5* Deseja-se investigar alteração no consumo de oxigênio em decorrência de uma certa moléstia que ataca o rim. Para indivíduos sadios, admite-se que esse consumo tem distribuição normal com média 12 cm^3 /min. Os valores medidos em cinco pacientes com moléstia foram: 14,4 ; 12,9 ; 15 ; 13,7 e 13,5. Qual seria a conclusão com nível de significância de 1%?
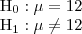
Deste modo, é obtida a seguinte região crítica:
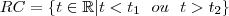
Ao contrário do teste para média com variância conhecida que calcula valores críticos para 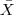 , vamos utilizar para construção da região crítica valores da estatística T.
, vamos utilizar para construção da região crítica valores da estatística T.
Os valores t1 e t2 são extremos sob H0 e tais que :
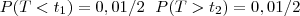
Com 4 graus de liberdade, estes valores são :
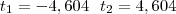
Repare que a simetria da distribuição normal se aplica também à distribuição t de Student. A Região Crítica (RC) é formada então pela união dos dois intervalos abaixo:
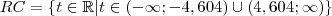
Para concluir sobre o teste, basta situar a posição da estatística observada em relação à Região Crítica.
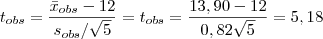
O valor 5,18 pertence a Região Crítica, logo esta amostra de tamanho n=6 fornece evidências a favor da hipótese alternativa. Logo, rejeitamos H0, sob o nível de significância de 1%.