Uma das questões que é levantada entre pesquisadores de diversas áreas diz respeito a associação entre variáveis. Veja alguns casos:

• A velocidade do atleta está associada com sua massa muscular ?
• A venda diária de refrigerantes está associada a temperatura máxima ?
• A nota de matemática de um aluno está associada a sua nota em física ?

Exemplo 5.3: Dentre os alunos do 1o ano do ensino médio de uma certa escola, selecionou-se os quinze alunos com melhor desempenho (nota acima de 7) em inglês. Veja na tabela abaixo as notas em inglês, português e matemática destes quinze alunos.

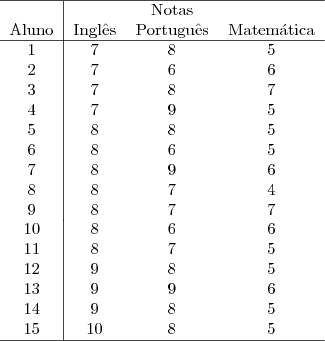
Para uma análise inicial da associação entre duas variáveis quantitativas, o diagrama de dispersão é a ferramenta indicada. O diagrama de dispersão consiste em exibir no plano cartesiano os pares de valores observados para duas variáveis quantitativas.

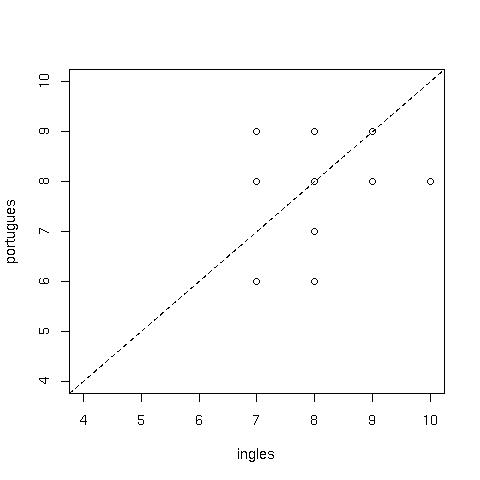
Figura 5.1- Diagrama de dispersão entre notas de inglês e português

Na Figura 5.1 é apresentado um diagrama de dispersão entre as notas de inglês e as notas de português dos 15 alunos. A reta tracejada indica qual seria o comportamento teórico se a associação entre as duas notas fosse perfeita, ou seja, se o alunos tivessem obtido as mesmas notas em português e inglês. A reta é referência para avaliar o comportamento dos alunos. Aqueles que tiveram desempenho melhor em português do que inglês estão acima da reta e os outros, que tiveram melhor desempenho em inglês, estão abaixo da reta.

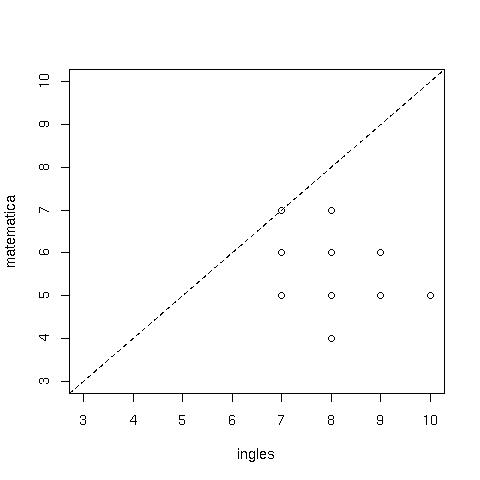
Figura 5.2- Diagrama de dispersão entre notas de inglês e matemática

Um novo diagrama de dispersão (Figura 5.2) ilustra a associação entre as notas de inglês e matemática. Nesta figura, revela-se a tendência dos alunos com bom desempenho em inglês apresentarem mau desempenho em matemática.

Embora o diagrama de dispersão seja uma importante ferramenta para visualizar a associação entre duas variáveis quantitativas, há algumas limitações no seu uso. Para citar uma delas, se no conjunto de dados o par (x,y) é repetido várias vezes, este fato não é ilustrado no diagrama de dispersão, a menos da utilização de uma intervenção gráfica como registrar o número de observações correspondente ao ponto (x,y).

Para representar objetivamente o grau de associação entre valores observados para duas variáveis quantitativas, utiliza-se com frequência a medida chamada de coeficiente correlação.

Para um conjunto de dados com n pares de valores (x,y) para as variáveis X e Y , a dependência (grau de associação) linear é medida através do coeficiente de correlação linear definido através de:

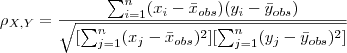
de forma mais conveniente este coeficiente pode ser reexpresso como:

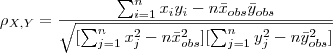
O coeficiente de correlação é uma medida adimensional que varia de -1 até 1. Quanto mais próximo dos extremos, maior é a evidência de asssociação entre as variáveis. Caso o coeficiente de correlação seja igual a zero, não há dependência linear entre as variáveis.

Exemplo 5.11: A quantidade de chuva é um fator importante na produtividade agrícola. Para medir esse efeito foram anotados, para 8 diferentes regiões produtoras de soja, o índice pluviométrico em milímetros (X) e a produção do último ano em toneladas (Y). Vamos determinar o coeficiente de correlação.

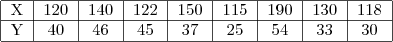
Para calcular o coeficiente de correlação entre o índice pluviométrico e a produção agrícola, através da segunda das formulações apresentadas, são necessários os seguintes somatórios:

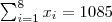
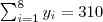
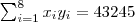
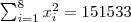
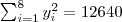
a substituição destes resultados na fórmula, gera o coeficiente :

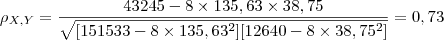
note que o valor próximo a 1, expressa associação positiva indicando que o aumento da quantidade de chuva está associado com aumento da produção.