Essa é uma revisão anterior do documento!
CE-003 Turma O - Primeiro semestre de 2012
No quadro abaixo será anotado o conteúdo dado em cada aula do curso.
São indicados os Capítulos e Sessões correspondentes nas referências bibliográficas do curso,
bem como exercícios sugeridos destes livros.
Abaixo da tabela há ainda Atividades Complementares.
Referências
- B & M: BUSSAB, W.O. & MORETTIN, P.A. Estatística Básica. 5a Edição, Editora Saraiva
- M & L: MAGALHÃES, M.N.; LIMA, A.C.P. Noções de Probabilidade e Estatística. IME/SP. Editora EDUSP.
- WEB Online Statistics: An Interactive Multimedia Course of Study: Material online sobre estatística
Observação sobre exercícios recomendados os exercícios indicados são compatíveis com o nível e conteúdo do curso.
Se não puder fazer todos, escolha alguns entre os indicados.
Conteúdos das Aulas
| B & M | M & L | Online | ||||
|---|---|---|---|---|---|---|
| Data | Conteúdo | Leitura | Exercícios | Leitura | Exercícios | Tópico |
| PARTE I: ESTATÍSTICA DESCRITIVA E ANÁLISE EXPLORATÓRIA DE DADOS | ||||||
| 05/03 | Informações sobre o curso. Apresentação das três partes do curso: estatística descritiva, probabilidades e inferência estatística Obtenção de dados: estudos experimentais e observacionais. Uma discussão introdutória sobre amostragem. Introdução a organização e análise descritiva de dados. | Cap 1 e 2 | – | Cap 1 | — | No material online ver: I . Introduction |
| 07/03 | Informações adicionais sobre o curso. Análise descritiva de dados (cont.) Tipos de variáveis (qualitativas nominais e ordinais, quantitativas discretas e contínuas). Uso de gráficos, tabelas e medidas no resumo de dados. Gráficos para análises uni e bi-variadas Demonstração computacional e introdução ao uso do R. | Cap 2 e 3 | Cap 3: 1 a 6 | Cap 4 | Sec 4.2: 1 a 3 | Material oline: Graphing Distributions |
| 12/03 | 1a Avaliação Semanal (AS) Análise descritiva de dados (cont.) Uso de gráficos, tabelas e medidas no resumo de dados. Análises uni e bi-variadas Medidas estatísticas para análises uni: medidas de posição, dispersão | Cap 2 e 3 | Cap 2: 2, 4, 6, 7 | Cap 1 e cap 4 | Sec 1.2: 1 a 5 , | Um exemplo de passos e comandos para análises descritivas |
| 14/03 | Análise descritiva de dados (cont.) Medidas estatísticas resumindo dados\\Medidas centrais: moda, mediana, média\\outras médias: geométrica, harmônica, aparada, generalizada e ponderada \\medidas de dispersão: amplitude, variância e desvio padrão, desvio médio, quartis e amplitude interquartílica\\outros tópicos: quantis (decis, percentis, etc), escores padronizados | Cap 3 | Cap 3: 1 a 6, 7, 11, 12, 13, 16 | Cap 4 | Sec 4.2: 1 a 3, Sec 4.3: 1 a 3, Sec 4.4: 1 a 7 | Material online: Summarizing Distributions |
| 19/03 | 2a avaliação semanal (AS) Análise descritiva de dados (cont.) Variáveis indexadas pelo tempo - séries temporais \\Pontos a serem observados em gráficos temporais | |||||
| 21/03 | Análise descritiva de dados (cont.) Análises bivariadas: qualitativa x qualitativa, quantitativa x qualitativa, quantitativa x quantitativa gráficos, tabelas e medidas medidas de associação: chi-quadrado e coeficientes de contingência, comparações de grupos (médias etc) e coeficientes de correlação | Cap 4 | Cap 4: 1 a 15 | Cap 5, Sec 5.2 (ver tb B&M) | Material online: Describing Bivariate Data |
|
| PARTE II: PROBABILIDADES E VARIÁVEIS ALEATÓRIAS | ||||||
| 26/03 | 3a avaliação semanal Introdução a probabilidades Experimentos aleatórios, eventos Definições (clássica, frequentista, subjetiva e axiomática). Propriedades de probabilidade Probabilidade de união, intercecção e condicional. Eventos mutuamente exclusivos e independentes | Cap 5 | Cap 5: 1 a 14 | Cap 2 | Sec 2.1: 1 a 5, Sec 2.3: 1 a 7 | Material Online: Probability (Itens A, B, C, D, E) |
| 28/03 | Probabilidades: discussão do vídeo de Peter Donnelly probabilidades marginais, conjuntas e condicionais. Probabilidade total e Teorema de Bayes. Exemplos exercícios | Cap 5 | Cap 5: 15 a 25 | Cap 2 | Sec 2.2: 4 a 7, Sec 2.3: 8 a 15 | Material Online: Probability (Itens H, I, J, K) |
| 02/04 | 4a avaliação semanal. Probabilidades: problemas e paradoxos. Ilustração computacional e simulação | Cap 5 | Cap 5: 26 a 41 | Cap 2 | Sec 2.3: 16 a 29 | Arquivo de comandos usado na aula |
| 04/04 | Variáveis aleatórias: introdução. Variáveis aleatórias discretas. Distribuições Uniforme, Binomial, Geométrica, Binomial Negativa (Pascal) e Hipergeométrica | Cap 6 | Cap 6: 1 a 6, 20, 21 , 25 | Cap 3 | Sec 3.2: 1 a 7 | Material online: Binomial Material online: Binomial (2) Material online: hipergeométrica |
| 09/04 | 5a avaliação semanal. Variáveis aleatórias discretas. função de probabilidades e função acumulada. Esperança e variância. Exemplos. | Cap 6 | Cap 6: 7, 8, 11, 13, 17, 29 a 33 | Cap 3 | Sec 3.1: 1 a 6, Sec 3.3: 1 a 6 | |
| 11/04 | v.a. discretas: distribuição de Poisson. Aplicações e exemplos. Processo de Poisson, suas características e aplicações. Introdução a v.a. contínuas. Definições, f.d.p.. Exemplo | Cap 6 e Cap 7 | Cap 6: 22, 23, 24, 34 a 40 e 56, Cap 7: 1 a 4 | Cap 3, Cap 6 | Sec 3.4: 1 a 28, Sec 6.1: 1 a 6 | Material online: Distribuição de Poisson |
| 16/04 | 6a avaliação semanal. V.A. contínuas: Exemplos exercícios, esperança, variância, função acumulada F(x) | Cap 7 | Cap 7: 5 a 12, 13, 21 | Cap 6 | Sec 6.2: 1 a 6, Sec 6.3: 1 a 24 | |
| 18/04 | V.A. contínuas: Exemplos. Distribuições uniforme, exponencial e normal | Cap 7 | Cap 7: 13 a 20 | Cap 6 | Sec 6.2: 7 a 9, Sec 6.3: 25 a 33 | Material online: Distribuição Normal |
| 23/04 | V.A. contínuas: Exemplos e distribuição normal | Cap 7 | Cap 7: 13 a 20 | Cap 6 | Sec 6.2: 7 a 9, Sec 6.3: 25 a 33 | |
| 25/04 | 2a prova | |||||
| 30/04 | feriado | |||||
| 02/05 | V.A. contínuas: outras distribuições: Gama, Beta, Weibull, F, t, chi-quadrado. Exemplos computacionais e exercícios | |||||
| 07/05 | 7a avaliação semanal | |||||
| 09/05 | sem aula presencial | |||||
| 14/05 | Noções de processos estocáticos: exemplos e definição, tempos e estados (discretos e contínuos), modelo probabilístico. Processos de tempo e estados discretos: Cadeia de Markov. Cadeias Finitas, probabilidades de transição, estacionaridade. Matrizes de transição e matrizes estocásticas, transição em M passos, vetor inicial, probabilidades marginais e estados absorventes. | ver sessão de complementos desta página | – | – | – | ver abaixo |
| 16/05 | Introdução a inferência. População e amostra - relações com distribuições de probabilidades. Estimação: estimadores e estimativas. Estimação por máxima verossimilhança. Exemplos. | Cap 10. 10.1, 10.2, 10.3. Cap 11: 11.5. | Cap 11: 10, 11, 12, 13 | Ver B&M | Ver B&M | |
| 17/09 | Informações sobre a retomada do semestre. sem aula com conteúdo | |||||
| 19/09 | Revisão dos temas das Partes I e II do curso (est. descritivas e probabilidades). Revisar materiais, provas e testes semanais. Dúvidas/perguntas no LEG | |||||
| 24/09 | Teste semanal e continuação - fundamentos de inferência estatística - estimação, incerteza, intervalos de confiança e testes de hipótese | Ler capítulos 10, 11 e 12 | Lar Cap 7 e 8 | |||
| 26/09 | Estimação e distribuições amostrais | Cap 10 | Cap 7 | |||
Materiais Complementares
05/03
- Material perdisco: Vídeo 1: Um vídeo introdutório sobre conceitos e temos básicos em estatística (legenda (CC) disponível)
- Guia:
- Quais os tópicos principais da apresentação? Descreva cada um deles com suas próprias palavras.
- Em cada tópico quais os principais conceitos? Identifique os termos técnicos e defina cada um deles.
- Pense em outros exemplos análogos aos apresentados no vídeo.
07/03
- Material perdisco: Vídeo 2: visualização de dados
- Arquivo com comandos para análises de desempenho em um curso
12/03
- Material perdisco: medidas que resumem dados
- Arquivo com comandos para análises de características de veículos
14/03
- Material perdisco: Vídeo 3: medidas que resumem dados
19/03
- Hans Rosling no TED Talks - como os dados podem nos ajudar a compreender e destruir mitos sobre a realidade. Procure identificar ao menos cinco pontos importantes na apresentação para discussão.
- Comandos com alguns exemplos de séries temporais discutidos em aula
21/03
- arquivo de comandos revisado (dados mtcars)
- A partir da próxima aula vamos iniciar a segunda parte do curso que trata de probabilidades. Como introdução e motivação, assistam antes da aula:
- Peter Donelly no TED Talks - como estatística e probabilidade podem ser usadas e … abusadas
- note que voce pode habilitar legendas em inglês, português ou outras línguas, se desejar
- procure anotar as principais mensagens e conceitos da apresentação
- se voce tivesse que destacar a descrever 2 (dois) pontos principais da apresentação, quais seriam?
26/03
- Material perdisco: Vídeo 4: Introdução a probabilidades
16/04
- Material perdisco: Vídeo 5: Distribuição de probabilidades (v.a. contínuas: 5:50 até final)
14/05
- Considere a matriz de transição do exemplo de preferência por produto da aula. Escreva um programa para simular realizações desta cadeia (mostre resultados em um gráfico).
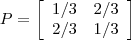
- Considere agora uma matriz de transição mais geral dada a seguir. Generalize seu programa do exemplo anterior e obtenha simulações para diferentes valores de
p. Escreva ainda uma rotina que receba os dados de uma cadeia e retorne uma estimativa dep. Use esta rotina para obter valores estimados deppara suas diferentes simulações (com o mesmope variandop)
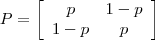
- Idem anterior com
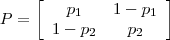
- Escreva agora uma rotina que calcule as probabilidades dos estados da cadeia em um passo (tempo) qualquer, a partir da matriz de transição e de um vetor
de probabilidades iniciais. Experimente (por simulação) com diferentes valores de
Pe - Idem anterior para um determinado inicial.
- Resuma as conclusões que podem ser obtidas analisando os resultados das simulações anteriores
Parte 2
- Estude o comportamento da cadeia definida pela seguinte matriz de transição.

- Modificar a matriz P dada colocando na ultima linha:
(0 0 0 0 0 1). Estude o comportamento da cadeia. - Estude o comportamento da cadeia com matriz de probabilidade de transição dada por

Parte 3
Suponha que o tempo predominante no dia em uma cidade vai ser classificado simplesmente como "nublado" ou "ensolarado". Suponha também que as condições do tempo em uma seqüencia de dias formam uma Cadeia de Markov com as seguintes probabilidades estacionárias.
| Ensolarado | Nublado | |
| Ensolarado | 0.7 | 0.3 |
| Nublado | 0.3 | 0.7 |
Com estes dados, responda:
- Se está nublado em um certo dia, qual a probabilidade de também estar nublado no dia seguinte?
- Se está ensolarado em um certo dia, qual a probabilidade de também estar ensolarado nos dois dias seguintes?
- Se está nublado em um dia, qual a probabilidade de ocorrer ao menos um dia ensolarado nos próximos tres dias?
- Se está ensolarado em uma certa quarta-feira, qual a probabilidade de também estar ensolarado no sábado seguinte?
- Se está nublado em uma certa quinta-feira, qual a probabilidade de também estar ensolarado no sábado seguinte?
- Se está ensolarado em uma certa quarta-feira, qual a probabilidade de também estar ensolarado no sábado seguinte?
- Se está ensolarado em uma certa quarta-feira, qual a probabilidade de também estar ensolarado em todo final de semana seguinte?
- Se está nublado em uma certa sexta-feira, qual a probabilidade de também estar ensolarado em todo final de semana seguinte?
- Suponha agora que a probabilidade de estar ensolarado em uma certa quinta-feira é de 0,2 (portanto de 0,8 de estar nublado)
- qual a probabilidade de estar nublado na sexta-feira seguinte?
- qual a probabilidade de estar nublado no domingo seguinte?
- qual a probabilidade de estar ensolarado no sábado e no domingo seguintes?