Essa é uma revisão anterior do documento!
CE-003 Turma K/O - Segundo semestre de 2013
No quadro abaixo será anotado o conteúdo dado em cada aula do curso.
São indicados os Capítulos e Sessões correspondentes nas referências bibliográficas,
bem como os exercícios sugeridos.
Veja ainda depois da tabela as Atividades Complementares.
Referências
- B & M: BUSSAB, W.O. & MORETTIN, P.A. (2010) Estatística Básica. 6a Edição, Editora Saraiva
- WEB Online Statistics: An Interactive Multimedia Course of Study: Material online sobre estatística
Observação sobre exercícios recomendados os exercícios indicados são compatíveis com o nível e conteúdo do curso.
Se não puder fazer todos, escolha alguns entre os indicados.
Conteúdos das Aulas
| B & M | Online | |||
|---|---|---|---|---|
| Data | Conteúdo | Leitura | Exercícios | Tópico |
| 26/08 Seg | Informações sobre o curso. Percepções sobre estatística e os fundamentos das três partes deste curso: (i) probabilidades, (ii) estatística descritiva e (iii) inferência estatística | Cap 1 | | ver abaixo |
| PARTE I: PROBABILIDADES | ||||
| 28/08 Qua | Introdução a probabilidades. Definições e conceitos básicos. Experimentos aleatórios, eventos, espaços de probabilidades, definições de probabilidades. Propriedades. | Cap 5, 5.1, 5.2 e 5.3 | Cap 5: 1 a 22 | Ver abaixo |
| 02/09 Seg | 1a avaliação semanal. Probabilidades (cont). Discussão da avaliação e revisão de conceitos. Tipos de espaço amostral e avaliação de probabilidades - a necessidade de modelos de probabilidade | Cap 5, 5.1, 5.2 e 5.3 | Cap 5: 1 a 22 | Material Online: Probability (Itens A, B, C, D, E) Ver outras indicações abaixo |
| 04/09 Qua | Probabilidades (cont.) Exemplos de espaços amostrais. Probabilidade condicional, probabilidade total e teorema de Bayes | Cap 5, 5.4 e 5.5 | Cap 5: 23 a 25, 26 a 41, 44, 48, 57 e 64 | Ver abaixo Ver exercícios no Cap 2 |
| 09/09 Seg | 2a avaliação semanal. Discussão da avaliação. Discussão do vídeo. Avaliação de probabilidades por simulação. | Cap 5 | Cap 5:ver indicados acima e nos materiais/referências suplementares | Ver abaixo |
| 11/09 Qua | Variáveis aleatórias discretas e contínuas. Introdução e definições. Funções de probabilidade, densidade de probabilidade, acumulada. Esperança e variância. Exemplos | Cap 6: Sec 6.1 a 6.5, Cap 7: Sec 7.1 a 7.3 | Cap 6: 1 a 19, 29, 30, Cap 7: 1 a 12 | |
| 16/09 Seg | 3a avaliação semanal. Discussão da avaliação. Exemplos e conceitos adicionais em variáveis discretas e contínuas. Obtenção de quantis. | |||
| 18/09 Qua | Distribuições "especiais" de v.a.'s discretas e contínuas. Binomial, Poisson, Gemétrica, uniforme e exponencial. Formas das distribuições normal e gama e interpretação do comportamento das variáveis. | Cap 6: Sec 6.6 e Cap 7, Sec 7.4 | Cap 6: 20, 21, 25, 26, 27, 28; Cap 7: 13, 21 | |
| 23/09 Seg | 4a avaliação semanal. Exemplos e visualizações do comportamento de variáveis discretas e contínuas. Discussão sobre algumas aplicações. | |||
| 25/09 Qua | Distribuição normal | Cap 7, Sec 7.4.2 e 7.5 | Cap 7: 14 a 20 | Material online Ver abaixo |
| 30/09 Seg | 5a avaliação semanal. distribuição normal. | |||
| 02/10 Qua | Aproximação pela distribuição normal, distribuições Hipergeométrica e de Poisson. Processo de Poisson. | Cap 6: 6.6.4, 6.6.5 e 6.7, Cap 7 | Cap 6:20, 22, 23, 34 a 38 | |
| 07/10 Seg | 6a avaliação semanal. Transformação de variáveis | Cap 7, Sec 7.6 | Cap 7: 25, 26, 27, 39, 43, 44 | |
| PARTE I: ESTATÍSTICA DESCRITIVA | ||||
| 09/10 Qua | Descrevendo e resumindo dados. Tipos de variáveis: qualitativas (nominais e ordinais) e quatitativas (discretas e contínuas). Resumo de dados por gráficos tabelas e medidas adequados a cada tipod e variável. Análises uni (perfil dos dados) e bivariadas (relações de interesse). | Cap 1, 2 e 3 | Cap 2: 1, 2 4 a 7, Cap 3: 1 a 6 | Ilustrações de análises uni e bivariadas |
| 14/10 Seg | Estatística descritiva (cont). Gráficos: histogramas, densidade, box-plot e ramo e folhas. Análises bivariadas. Qualitativas x quantitativas e quantitativas vs quantitativas. Medidas e formas de associação. | Cap 2, 3 e 4 | Cap 2: 4 a 8, Cap 3: 7 a 13, Cap 4: 1,2,3,10,11 | |
| 16/10 Seg | 1a prova | |||
| 21/10 Seg | 7a avaliação semanal. Discussão da avaliação e medidas descritivas. Posição, dispersão, assimetria e curtose | Cap 3 | Cap 3: 14 a 29, 33, 34, 35, 38, 39, 40 | Ver abaixo |
| 24/10 Qua | Tópicos complementares em estatística descritiva. | Ver abaixo | ||
| 28/10 Seg | Aula de estudos | |||
| 30/10 Qua | Estatística descritiva (cont). Associação entre variaveis qualitativas, Chi-quadrado, risco relativo e razão de chances (odds–ratio). q-q plots para comparação de variáveis. | Cap 4 | ||
| PARTE III: ESTATÍSTICA DESCRITIVA | ||||
| 04/11 Seg | 8a avaliação semanal. Introdução a inferência estatística: população, amostra, parâmetro, estimador, estimativa, distribuição amostral, estimativa pontual e por intervalo, tamanho de amostra | Cap 10 | Cap 10: 17, 18, 21 a 28 | |
| 06/11 Qua | Inferência estatística (cont): construção de distribuições amostrais e distribuição amostral da média (e proporção). Tamanho de amostra. Intervalo de confiança (para proporção) | Cap 10, Cap 11, Sec 11.1 e 11.6 | Cap 10: 1, 3, 4 a 6, 11 a 13, 18, 20 e 21 | |
| 10/11 Seg | 9a avaliação semanal. Discussão da avaliação e introdução a conceitos básicos sobre testes (estatístico) de hipótese: definição, hipóteses nula e alternativa, região crítica, nível de significância, erros tipo I e II. Exemplo: teste de hipótese para uma proporção | Cap 12 Sec 12.1 e 12.2 e 12.6 | Cap 12: 1 a 5, 10 a 13, 17, 18 | |
| 13/11 Qua | Inferência estatística (cont): distribuições amostras da média e outras distribuições amostras. Exercícios e aplicações. Propriedades dos estimadores. Intervalos de confiança para média. | Cap 10, Cap 11, Sec 11.1 e 11.2 | Cap 10: 1 a 5, 14 a 17 | |
| 18/11 Seg | 10a avaliação semanal. Discussão da avaliação: distribuições amostrais, intervalos de confiança e teste de hipótese. | |||
| 20/11 Qua | Inferência estatística (cont): propriedades dos estimadores (consistência, não viés e eficiência) e erro quadrático médio. Métodos de estimação: momentos, mínimos quadrados e máxima verossimilhança | Cap 11 | Cap 11: 10, 11, 12, 13 | |
| 25/11 Seg | 11a avaliação semanal. Testes Chi-quadrado | Cap 14 | Cap 14: | |
| 27/11 Qua | Comparação de duas amostras (variâncias e médias) | Cap 13 | Cap 13: | |
| 02/12 Seg | não haverá aula - sala ocupada com 2a fase vestibular | |||
| 04/12 Qua | ||||
| 09/12 Seg | 2a prova | |||
| 18/12 Qua | Prova Final | |||
Atividades complementares
26/08
- Dois jogadores A e B vão jogar várias rodadas do seguinte jogo:
Cada vai lançar um dado e o resultado será a soma das faces. Antes do lançamento cada um escolhe um dos resultados possíveis. Se voce fosse definir uma estratégia para aconselhar um dos jogadores, qual seria? Justifique!
28/08
- Material perdisco: Vídeo 1: Um vídeo introdutório sobre conceitos e temos básicos em estatística (legenda (CC) disponível)
- Guia:
- Quais os tópicos principais da apresentação? Descreva cada um deles com suas próprias palavras.
- Em cada tópico quais os principais conceitos? Identifique os termos técnicos e defina cada um deles.
- Pense em outros exemplos análogos aos apresentados no vídeo.
02/09
- Peter Donelly no TED Talks - como estatística e probabilidade podem ser usadas e … abusadas
- note que voce pode habilitar legendas em inglês, português ou outras línguas, se desejar
- procure anotar as principais mensagens e conceitos da apresentação
- se voce tivesse que destacar a descrever 2 (dois) pontos principais da apresentação, quais seriam?
- formule adequadamente e tente resolver os problemas propostos durante a palestra
Considere os problemas a seguir e resolva cada uma deles de duas formas:
- Solução formal (analítica)
- Solução (aproximada) por alguma rotina computacional
- Um comitê de 12 pessoas é escolhido por sorteio de um grupo de 100 pessoas. Calcule a probabilidade dos indivíduos A e B pertencerem os grupo escolhido.
- Um baralho de 52 cartas contém 4 cartas do tipo ás. Se as cartas são embaralhadas e 13 cartas são divididas entre 4 indivíduos, qual a probabilidade de que algum deles fique com todas as cartas ás.
- Se n pessoas terão seus assentos atribuídos ao acaso em uma linha com 2n assentos, qual a probabilidade que não haja pessoas em assentos adjacentes?
09/09
- Propor um algorítmo computacional para estudar por simulação) o problema das sequencias de caras e coroas apresentado no vídeo Peter Donelly
- Resolver o problema das portas (Monty Hall):
- resposta analítica
- resposta por simulação computacional (escrever algoritmo)
Considere postar/compartilhar seus algorítmos na Página do Espaço Aberto do Curso
25/09
Comandos no programa R para cálculos relacionados a distribuição normal
Seja uma v.a. 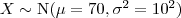
Leituras e Exercícios extras- Probabilidades
- Exercícios para revisão (compatíveis com ensino médio):
- Exercícios sobre conceitos básicos de cálculo de probabilidades sugeridos para uma revisão inicial
- Exercícios na web procure identificar espaço amostral, eventos e demais conceitos discutidos em aula
- Textos sobre probabilidades (com exercícios)
- Capítulo 1 do Livro do Prof. Caio Dantas
21/10
- Verificar a definição e aplicações de média geométrica e média harmônica
- verificar como calcular e interpretar os coeficientes de assimetria e curtose
24/10
- Hans Rosling no TED Talks - como os dados podem nos ajudar a compreender e destruir mitos sobre a realidade. Procure identificar ao menos cinco pontos importantes na apresentação para discussão (com opção de legendas em português).