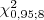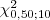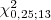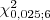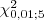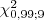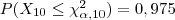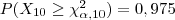Essa é uma revisão anterior do documento!
Tabela de conteúdos
CE-003 Turma A - Segundo semestre de 2010
No quadro abaixo será anotado o conteúdo dado em cada aula do curso.
É indicado material para leitura correspondente ao conteúdo da aula nas referências bibliográficas básicas do curso:
- B & M: BUSSAB, W.O. & MORETTIN, P.A. Estatística Básica. 5a Edição, Editora Saraiva
- M & L: MAGALHÃES, M.N.; LIMA, A.C.P. Noções de Probabilidade e Estatística. IME/SP. Editora EDUSP.
- A & O: ANDRADE, D,F; OGLIARI, P.J. (2007) Estatística para as Ciências Agrárias e Biológicas (com noções de experimentação). Editora da UFSC.
- Online Online Statistics: An Interactive Multimedia Course of Study: Material online sobre estatística
| B & M | M & L | A & O | Online | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | Local | Conteúdo | Leitura | Exercícios | Leitura | Exercícios | Leitura | Exercícios | Tópico | ||
| 09/08 | PD-02 | Informações sobre o curso. Introdução e organização à disciplina. Estatística: onde, quando, por que e para que?. Os três temas do curso: estatística descritiva, probabilidades e inferência, ideias básicas e exemplos | Cap 1 | – | Cap 1 | — | Cap 1 | — | |||
| 11/08 | – | Não haverá aula presencial. Leitura e estudos: ver atividades abaixo | Cap 1 | – | Cap 1 | — | Cap 1 | — | Chapter 1, Sections A, B, C e D | ||
| 16/08 | PD-02 | Probabilidades: motivação, problemas e desafios. Experimentos aleatórios. Espaço amostral (equiprovável?, finito?, enumerável?). Eventos aleatórios. Definições de probabilidade: axiomática, clássica, freqüentista, subjetiva. | Cap 5 Sec 5.1 | Cap 5, 1 a 5 | Cap 2, Sec 2.1 | Cap 2, Sec 2.1: 1 a 5 | Cap 3, Sec 3.1 | Cap 3: 1 a 3 | Capter 5, Section A e B | ||
| 18/08 | – | Não haverá aula presencial. Leitura e estudos: ver atividades abaixo | — | – | — | — | — | — | — | ||
| 23/08 | PD-02 | Probabilidades, definições, propriedades. Eventos mutuamente exclusivos. Probabilidade condicional e independência | Cap 5: Sec 5.1 a 5.3 | Cap 5: 7 a 22 | Cap 2: Sec 2.1 e 2.2 | Cap 2: Sec 2.2, 1 a 7 | Cap 3: Sec 3.1 a 3.7 | Cap 3: 1, 4 a 19 | Capter 5, Section C, D, E | ||
| 25/08 | PD-02 | Probabilidades: teorema da probabilidade total, teorema de Bayes, Exercícios | Cap 5 | Cap 5: 23 a 25 | Cap 2 | Cap 2, Sec 2.3: 21 e 22 | Cap 3 | — | Chapter 5, Section I, J, K | ||
| 30/08 | PD-02 | Probabilidades: discussões de problemas e exemplo. Variáveis aleatórias discretas e contínuas: introdução, motivação, definições, notação, propriedades. Função de probabilidade (discretas) e função de densidade de probabilidades (contínuas) | Cap 6, Sec 6.1 e 6.2; Cap 7, Sec 7.1 | Cap 6: 1 a 6; Cap 7: 1 a 4 | Cap 3, Sec 3.1; Cap 6, Sec 6.1 | Cap 3, Sec 3.1: 1 a 7; Cap 6, Sec 6.1: 1 a 5 | Cap 4, Sec 4.1; Cap 5, Cap 5 | Cap 4: 1 e 2 | — | ||
| 01/09 | PD-02 | Variáveis aleatórias discretas e contínuas: esperança, variância. Distribuições acumuladas. Exemplos e exercícios | Cap 6, Sec 6.3 a 6.5; Cap 7, Sec 7.2 e 7.3 | Cap 6: 7 a 17; Cap 7: 5 a 10 | Cap 3, Sec 3.1; Cap 6, Sec 6.1 | Cap 3, Sec 3.1: 1 a 7; Cap 6, Sec 6.1: 1 a 5 | Cap 4, Sec 4.1; Cap 5, Cap 5 | Cap 4: 1 e 2 | — | ||
| 13/09 | PD-02 | Distribuições de variáveis aleatórias discretas: uniforme, Bernoulli, binomial, geométrica, binomial negativa (Pascal), hipergeométrica e Poisson | Cap 6, Sec 6.6 | Cap 6: 20 a 24, 26, 27, 29-34, 37, 39, 42, 56 | Cap 3, Sec 3.2 e 3.3 | Cap 3, Sec 3.2: 1 a 7; Sec 3.3: 1 a 6 | Cap 4, Sec 4.4 e 4.5 | Cap 4: Ver exercícios resolvidos, exercícios Sec 4.6 | — | ||
| 15/09 | PD-02 | Distribuições discretas: exercícios. Distribuições de variáveis aleatórias contínuas: uniforme, exponencial | Cap 7, Sec 7.4.1, 7.4.3 | Cap 7: 13, 21, 31, 40, 41 | Cap 6, Sec 6.2 (uniforme e exponencial) | Cap 6, Sec 6.2: 1 a 6, Sec 6.3: 16 a 24 | — | ||||
| 20/09 | PD-02 | Dúvidas, exercícios e revisão para prova I | |||||||||
| 22/09 | PD-02 | Prova I | |||||||||
| 27/09 | PD-02 | Distribuição Normal (Gaussiana) | Cap 7, Sec 7.4.2 | Ca7 7: 14 a 20 | Cap 6, Definição 6.6 | Cap 6, Sec 6.2: 7 a 9 | Cap 5: Sec 5.2 | Cap 5: Sec 5.2.4: 1 a 10 | Chapter IV | ||
| 29/09 | PD-02 | Distribuição Normal (Gaussiana). Exercícios. | Cap 7, Sec 7.4.2 e 7.5 | Cap 7: 21 a 24, 33 a 38 | Cap 6, Definição 6.6 | Cap 6, Sec 6.3: 25 a 33 | Cap 5: Sec 5.2 | Cap 5: Sec 5.2.4: 11, 12, 14, 15, 18, 19, 22, 25, 26, 30 a 32 | Chapter IV | ||
| 04/10 | PD-02 | Distribuição Normal (Gaussiana). Exercícios, aplicações. Aproximação normal à distribuição binomial | Cap 7, Sec 7.4.2 e 7.5 | ver anterior | Cap 6, Definição 6.6 | ver anterior | Cap 5: Sec 5.2 | ver anterior | Chapter IV | ||
| 06/10 | PD-02 | Distribuição de funções de v.a. contínuas. Outras distribuições: Gamma, t, 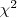 e F. Quantis e F. Quantis | Cap 7, Sec 7.6, 7.7 e 7.8 | Cap 7: 25, 26 (ver abaixo) | Ver em B&M | ver em B&M | ver em B&M | ver em B&M | |||
| 11/10 | – | Feriado | |||||||||
| 13/10 | PD-02 | Estatística descritiva: motivação, uso, objetivos, organização de dados, análises univariadas: tipos de variáveis (qualitativas nominais e ordinais, quantitativas discretas e contínuas). Gráficos, tabelas e medidas adequados a cada tipo de variável. | Cap 1, Cap 2, Sec 2.1, 2.2, 2.3 | Cap 2: 1, 2, 6, 7, 9 | Cap 1 | Cap 1, Sec 1.3: 1 a 3, Sec 1.4: 1 a 6 | Material com R na página do LEG | ||||
| 18/10 | PD-02 | Estatística descritiva (cont): distribuições de frequências, ramo e folhas, medidas descritivas, box-plot (Ver abaixo comandos do R para produzir gráficos mostrados em sala) | Cap 2: 2.4. Cap 3 | Cap 2:4, 5, 11, 19, Cap 3: 1 a 6 | Cap 1, Cap 4 | Cap 1: 7 a 22 | Material online: Graphing distributions | ||||
| 20/10 | PC-19 | Estatística descritiva (cont): medidas de posição e dispersão | Cap 3 | Cap 3: 8 a 10, 16, 19 a 25, 29, 33, 35 | Cap 4 | Cap 4: 4.2: 1 a 6, 4.3: 1 a 6, 4.4: 1 a 9, 11 a 13 | Material online: summarizing distributions | ||||
Atividades do Curso
11/08
- Problemas para discussão:
- Desejamos saber a probabilidade de um casal ter duas filhas (meninas) em três situações distintas:
- apenas sabendo que eles tem duas crianças
- depois que o pai comenta que tem uma filha (sem dar mais detalhes, sem indicar se é a mais velha ou mais nova etc)
- voce encontra os amigos e eles estão com uma das crianças com eles que é uma menina
- Quantas pessoas devem haver em um grupo para que a chance de haver ao menos uma coincidência de aniversários supere 50% ?
- Dois jogadores (A e B) vão jogar um jogo que consiste no lançamento de dois dados. Ambos começam com R$ 10,00. Se a soma dos dados for um número ímpar, A para R$ 1,00 para B. Se a soma for par, B para R$ 1,00 para A.
- quais os possíveis valores em dinheiro que os jogadores podem ter após 2 rodadas? A chance é a mesma para todos esses possíveis valores?
- quais os possíveis valores em dinheiro que os jogadores podem ter após 3 rodadas? A chance é a mesma para todos esses possíveis valores?
- o jogo é honesto?
- Assista os vídeos a seguir, reflita, discuta com os colegas e em sala.
- Hans Rosling no TED Talks - como os dados podem nos ajudar a compreender e destruir mitos sobre a realidade
- Peter Donelly no TED Talks - como estatística e probabilidade podem ser usadas e … abusadas
- note que voce pode habilitar legendas em inglês, português ou outras línguas, se desejar
- procure anotar as principais mensagens de cada apresentação
- se voce tivesse que destacar a descrever 2 (dois) pontos principais em cada apresentação, quais seriam?
16/08/2010
- Leituras adicionais
- Sugestão de leitura adicional: Pags 15 a 38 Dantas (2008)
- Exercício adicional
- No vídeo de Peter Donnelly indicado acima, ele pede à audiência para imaginar o seguinte experimento aleatório jogando-se várias vezes uma moeda:
- (A) conta-se o número de jogadas até se obter a sequência cara-coroa-coroa (head-tail-tail - HTT),
- (B) conta-se o número de jogadas até se obter a sequência cara-coroa-head (head-tail-head - HTH).
Imagina-se que os experimentos (A) e (B) são repetidos muitas vezes e em cada uma anota-se o número de jogadas. Ao final calcula-se o número médio do número de jogadas anotadas em cada caso () e (
). A questão levantada pelo apresentador é o que se espera:
ou
ou
?
Tente encontrar a resposta e/ou entender o argumento do apresentador. Adicionalmente, escreva um programa computacional que simule este experimento e encontre a solução através desta simulação.
16/08/2010
- Ver(rever) atividades acima
- Lista de exercícios (em breve aqui)
23/08/2010
- Refazer o problema dos jogadores (A e B) no jogo de dados com as seguintes regras:
- se a soma for 7, A ganha e B para R$ 1,00 para A
- se a soma for 6, B ganha e A para R$ 1,00 para B
- para qualquer outro resultado não há ganhador
- Discuta com exemplos a diferença dos conceitos de eventos mutuamente exclusivos e eventos independentes
- Fazer um programa na linguagem computacional de sua preferência para avaliar por simulação o número médio de tentativas para obter HTT e HTH no problema apresentado por Peter Donnelly mencionado acima.
25/08/2010
- Voltar à discussão do teste de HIV apresentada no vídeo de Peter Donnelly. Representar o problema em notação correta seguindo o exemplo dado em sala de aula.
- No lançamento de três dados equilibrados, 9 e 10 pontos podem ser obtidos de seis maneiras diferentes:
Soma 9: 1 2 6, 1 3 5, 1 4 4, 2 2 5, 2 3 4, 3 3 3, e
Soma 10: 1 3 6, 1 4 5, 2 2 6, 2 3 5, 2 4 4, 3 3 4, respectivamente.
Como pode este fato ser compatível com a experiência que leva jogadores de dados a considerarem que a
soma 9 ocorre menos vezes que a soma 10?
- Ver o Material Online Online Statistics: An Interactive Multimedia Course of Study adicionado acima na lista de referências e os tópicos sugeridos na tabela de atividades do curso.
06/09/2010
EXERCÍCIOS ADICIONAIS: outras distribuições contínuas
- Considere uma v.a. com distribuição
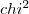 Obtenha (aproximando se necessário):
Obtenha (aproximando se necessário):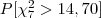
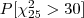
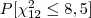
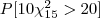
- o valor de tal que
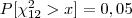
- o valor de tal que
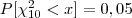
- o valor de tal que
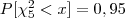
- o valor de tal que
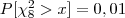
- Para a distribuição
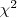 encontre os seguintes valores:
encontre os seguintes valores: - Para a distribuição
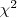 encontre os seguintes valores (quantis):
encontre os seguintes valores (quantis):
18/10/2010
dados <- c(3.67, 1.28, 3.96, 2.93, 7.77, 2.78,
1.82, 8.14, 6.54, 2.82, 4.65, 5.54,
3.73, 2.43, 5.84, 8.45, 1.88, 0.90,
4.10, 4.17, 7.35, 5.28, 2.12, 5.09,
4.30, 5.36, 3.63, 5.41, 4.26, 4.07)
summary(dados)
## Histogramas mostrados na aula:
## histograma com frequencias absolutas e intervalos de classe de 1 unidade
h1 <- hist(dados, breaks=seq(0, 9, by=1), main="")
# histograma com frequencias absolutas e intervalos de classe de 1,5 unidades
# e a ultima com duas unidades
h2 <- hist(dados, breaks=c(0.5, 2, 3.5, 5.0, 6.5, 8.5), main="")
plot(h1)
plot(h2)
## vendo as classes e frequencias em cada caso
h1[1:2]
h2[1:2]
## e vendo de outra forma
table(cut(dados, breaks=seq(0, 9, by=1)))
table(cut(dados, breaks=c(0.5, 2, 3.5, 5.0, 6.5, 8.5)))
## agora outros gráficos:
## histograma de probabilidades, histograma suavizado ("density plot") e marcação de dados ("rug")
hist(dados, main="", prob=TRUE)
rug(dados)
lines(density(dados))
## note que o density() nao depende da definicao de classes!
## ou simplesmente
plot(density(dados))
rug(dados)
## ramos e folhas
stem(dados)
## boxplot:
boxplot(dados)
Códigos R
- Instalar o programa R mencionado na página do curso e experimente com os comandos abaixo:
- O problema dos aniversários
"aniv" <- function(n, p){ if(missing(n) && missing(p)) error("um dos argumentos, n ou p deve ser fornecido") if(!missing(n) && !missing(p)) error("apenas um dos argumentos, n ou p deve ser fornecido") Prob <- function(n) 1 - exp(sum(log(365:(365-n+1))) - n*log(365)) VecProb <- Vectorize(Prob, "n") if(missing(n)) res <- sapply(p, function(y) which((VecProb(1:366) - y) > 0)[1]) if(missing(p)) res <- VecProb(n) return(res) } aniv(n=23) aniv(n=c(10, 20, 35, 50, 57)) aniv(n=366) plot(1:366, aniv(n=1:366), type="l", xlab="n", ylab="P[Coincidencia]") aniv(p=0.5) aniv(p=c(0.2, 0.4, 0.5, 0.7, 0.9, 0.99)) plot(1:100, aniv(n=1:100), type="l", xlab="n", ylab="P[Coincidencia]") arrows(c(1,aniv(p=0.5)),c(0.5, 0.5),c(aniv(p=0.5),aniv(p=0.5)),c(0.5,0), length=0.1) text(1, 0.5, 0.5, pos=2, off=0.1, cex=0.7) text(aniv(p=0.5),0 ,aniv(p=0.5), pos=1, off=0.2, cex=0.7) - O problema das sequências de caras e coroas
"nTenta" <- function(N, padrao="HTT", media = TRUE){ padrao <- strsplit(padrao, NULL)[[1]] nc <- length(padrao) nTenta <- numeric(N) for(i in 1:N){ res <- sample(c("H","T"), nc, rep=T) n <- nc while(any(res != padrao)){ res <- c(res[2:nc], sample(c("H","T"), 1, rep=T)) n <- n+1 } nTenta[i] <- n } if(media) return(mean(nTenta)) else return(nTenta) } nTenta(10000, "HTT") nTenta(10000, "HTH") - O problema da carta premiada (Monty Hall)
"jogo" <- function(){ cartas <- LETTERS[1:3] premio <- sample(cartas, 1) escolha <- sample(cartas, 1) sobra <- cartas[which(cartas != escolha)] mostra <- sample(sobra[which(sobra != premio)], 1) NTroca <- escolha Res.NT <- ifelse(NTroca == premio, "Ganhou", "Perdeu") Troca <- sobra[sobra != mostra] Res.T <- ifelse(Troca == premio, "Ganhou", "Perdeu") return(c(premio, escolha, mostra, NTroca, Res.NT, Troca, Res.T)) } set.seed(231) sim <- as.data.frame(t(replicate(10000, jogo()))) names(sim) <- c("premio", "escolha", "mostra", "NTroca", "Res.NT", "Troca", "Res.T") #sim prop.table(table(sim$Res.NT)) prop.table(table(sim$Res.T))
\begin{enumerate} \item (Dantas, 2008) Defina o espaço amostral para cada um dos seguintes experimentos aleatórios: \begin{enumerate} \item lançam-se dois dados e anota-se a configuração obtida \item conta-se o número de peças defeituosas, no intervalo de uma hora, em uma linha de produção \item investiga-se famílias com quatro crianças a anota-se a configuração obtida segundo o sexo \item em uma entrevista telefônica com dez assinantes, pergunta-se se o proprietário tem um não máquina de secar roupa \item de um fichário de seis nomes, sendo três homens e três mulheres, seleciona-se ficha após ficha até que o último nome de mulher seja selecionado % \item \end{enumerate} \item (Dantas, 2008) Suponha que o espaço amostral de um experimento aleatório seja o intervalo $[0,1]$ dos reais. Considere os eventos: $A=\[x : 1/4 \leq x \leq 5/8 \]$ e $B=\[x : 1/2 \leq x \leq 7/8 \]$. Determine os eventos: (a) $A^c$ ; (b) $A \cap B^c$ ; (c) (A \cup B)^c ; (d) $A^c \cap B$