A joint model proposal????

Ao olhar as simulacoes e a descrio de como eram feitas que vc me fez eu sempre achei muito complicado de explicar de forma breve e facil de entender. Resolvi entao pensar em uma outra forma mais direta de ferar simulacoes relacionando as proporcoes com a abundancia.

Tive entao a ideia de fazer segundo um modelo onde poderiamos controlar por parametros o que desejamos. Veja o seguinte e me diga o que acha:

1. Simular Y que representa a abundancia total

Daqui para frente seguem duas sequencias de possiveis procedimentos:

A. proporcoes como funcoes perfeitas de Y

A.2. Obter
      p1 <- exp(1*Y)/(1+exp(1*Y))
A.3  Obter
      p2 <- exp(0.5*Y)/(1+0.5*Y)
A.4  Obter
      p3 <- 2 - p1 - p2
A.5  Transformar p1, p2 e p3 em composicoes dovidindo cada um pela soma
     de todos eles

Neste caso note que p1 mais relacionado com Y, p2 menos varivel e p3 tem uma correlacao negativa com estes.

Poderia-se ainda somar (subtrair uma constante para forcar proporcoes mais altas ou baixas)

Para intuicao sobre os valores veja:

 y <- grf(100, cov.pars=c(1, .25))$data
 p1 <- exp(y)/(1+exp(y))
 range(p1)
[1] 0.1567524 0.8486654
 p2 <- exp(0.5*y)/(1+exp(0.5*y))
 range(p2)
[1] 0.3012618 0.7030963
 p2 <- exp(1+0.5*y)/(1+exp(1+0.5*y))
 range(p2)
[1] 0.5395928 0.8655399
 range(p1+p2)
[1] 0.6963451 1.7142053
 p3 <- 2 - p1 - p2
 pt <- p1+p2+p3
 p1 <- p1/pt; p2 <- p2/pt; p3 <- p3/pt
 plot(cbind(p1,p2,p3))

A de forrma geral transformacao e' dada por

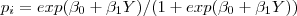
e os valores d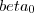e e 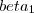controlam o comportamento e com isto poderia-se escolher qual a calsse a ser representada por cada um deles.

B. Semelhante a anterior porem adicionando uma aleatoriedade nas proporcoes B.2. Obter como anterior porem adicionando um "ruido", trocando Y no algoritmo anterior por

Y + rnorm(length(y), m=0, sd=0.1)

Depois fazer o mesmo para p2 e o resto fica como no algortmo anterior

E….. acho que acabo de inventar um novo modelo para modelagem conjunta!!!!!