Tabela de conteúdos
Medidas Resumo
Introdução
Em um processo de coleta de dados, através de amostragem ou censo, faz-se necessário resumir as informações contidas nas variáveis através de medidas adequadas. Neste capítulo estas serão chamadas medidas resumo.
Exemplo 4.1 Em um ponto de ônibus, uma pessoa pergunta sobre o tempo até a passagem de uma determinada linha. Suponha que você havia coletado ao longo da semana anterior, os tempos (em minutos) e registrado os seguintes resultados: 9; 12; 8; 10; 14; 7; 9. Para apontar a tendência central destes dados, você faz o uso da média e responde: "aproximadamente 10 minutos".
Neste exemplo, ilustra-se o papel de uma medida resumo para um conjunto de dados observados pois a média aritmética dos números acima é 9,86, e este resultado é utilizado na resposta.
Medidas de Posição (Tendência Central)
As medidas de posição também são conhecidas por medidas de tendência central. Estas são calculadas como a primeira síntese de uma variável. Aqui, mostraremos como calcular as principais medidas de posição: média, mediana e moda.
Medidas de posição (tendência central) para um conjunto de dados
Sejam as observações obtidas a partir da variável aleatória X, em uma população ou em uma amostra:
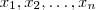
considere a seguinte notação para os dados ordenados:
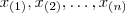
onde x(1) é o menor valor no conjunto de dados e x(n) é o maior valor. Então, a média, mediana e moda observada são calculadas conforme:
- Média Observada
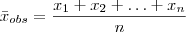
- Mediana Observada
 se n é impar
se n é impar
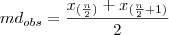 se n é par
se n é par
- Moda observada
A moda observada, aqui denotada por moobs é simplesmente o valor mais frequente em um conjunto de dados.
Medidas de Dispersão
Embora as medidas de posição forneçam uma primeira síntese dos dados, medir variabilidade é fundamental em qualquer análise estatística. A medidas de dispersão irão exercer este papel, ou seja, quantificar a incerteza presentes nos dados.
Tal como ocorreu para as medidas de posição, aqui serão apresentadas as medidas de dispersão numa situação em que dispõe-se de um conjunto de dados.
Serão apresentadas as medidas:
- amplitude
- desvio mediano (absoluto)
- desvio médio (absoluto)
- variância
- desvio padrão.
Medidas de dispersão para um conjunto de dados
Amplitude
A amplitude é a diferença entre a maior e menor observação em um conjunto de dados.
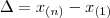
A grande deficiência desta medida está no fato de ser calculada em função de duas observações em um conjunto de n números. Caso os extremos sejam discrepantes em relação ao restante dos dados, a amplitude pode superdimensionar a variabilidade dos dados.
Desvio mediano
O desvio mediano é calculado em função das distâncias (desvios) das observações em relação à mediana. Deste modo, a i-ésima observação está distante da mediana pela expressão:
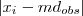
ao tomarmos a média destes desvios, temos a medida denominada desvio mediano.
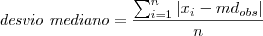
Desvio médio
Na medida desvio mediano, o desvio é calculado em relação à mediana. Entretanto, o conceito de desvio em estatística está mais relacionado à distância de uma observação em relação a média.
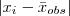
Sendo assim, a substituição da mediana pela média, e utilização do valor absoluto, vai fornecer a medida chamada desvio médio.
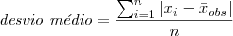
Variância
A variância é outra medida de dispersão calculada com base em desvios. Neste caso, serão considerados os desvios quadráticos em relação a média dados pela expressão :
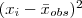
e ao tomar as médias destes desvios quadráticos, é obtida a variância.
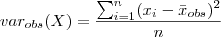
Desvio padrão
Por calcular desvios quadráticos, a variância é uma medida de difícil interpretação. Entretanto, ao tomarmos a raiz quadrada desta medida temos o desvio-padrão que retorna a escala original em que os dados foram medidos.
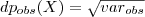
Exemplo 4.3 Sejam as quantidades de parafusos em 10 caixas de um lote: 98;102;100;100;99;97;96;95;99;100. A Tabela 4.1 exibe os valores dos desvios utilizados para calcular o desvio médio, a variância e o desvio padrão para este conjunto de dados.
Tabela 4.1 - Desvios, desvios absolutos e desvios quadráticos
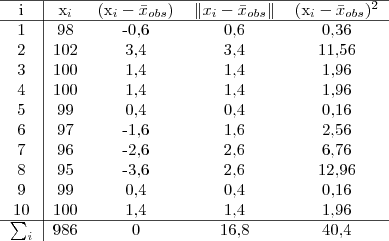
Na Tabela 4.1, coloca-se na última linha os totais referentes as somas dos valores em cada coluna. Dividindo estas somas pelo tamanho da amostra n=10, encontra-se :
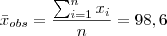
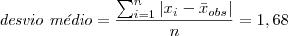
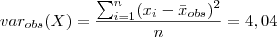
Após o cálculo da variância, é possível encontrar o desvio padrão, calculando-se a raiz deste número.
