Tabela de conteúdos
Introdução à Estatística descritiva e Análise exploratória de dados
O que é Estatística?
No dicionário Aurélio, encontra-se como a primeira definição para Estatística:
[Do fr. statistique.] S. f. 1. Parte da matemática em que se investigam os processos de obtenção, organização e análise de dados sobre uma população ou sobre uma coleção de seres quaisquer, e os métodos de tirar conclusões e fazer ilações ou predições com base nesses dados.
A Estatística é um conjunto de métodos de coleta e descrição de dados, e então a verificação da força da evidência nos dados pró ou contra certas idéias científicas.
Estes métodos foram desenvolvidos com a finalidade de auxiliar a responder, de forma objetiva e segura, problemas que envolvem uma grande quantidade de informações.
É notório que:
- A quantificação de toda espécie de informações tem aumentado nas últimas décadas e é parte do nosso cotidiano desde a popularização dos computadores.
- Grande quantidade de informações pode ser analisada rapidamente com um computador pessoal e programas adequados. O computador contribui positivamente na difusão e uso de métodos estatísticos.
- Tal automação pode levar um indivíduo sem preparo a utilizar técnicas inadequadas para resolver um dado problema.
Portanto, é necessário a compreensão dos conceitos básicos da Estatística, bem como as suposições necessárias para seu uso de forma criteriosa.
A presença de uma variação não previsível nos dados faz disso uma tarefa pouco trivial.
Exemplo: Variação amostral
Um exemplo em que a variação está presente nos dados:
Função pulmonar em pacientes com fibrose cística: A pressão inspiratória estática máxima (PImax) é um índice de vigor respiratório muscular. Os seguintes dados mostram a idade (anos) e uma medida de PImax (cm H2O) de 25 pacientes com fibrose cística.
| Sujeito | Idade | PImax |
| 1 | 7 | 80 |
| 2 | 7 | 85 |
| 3 | 8 | 110 |
| 4 | 8 | 95 |
| 5 | 8 | 95 |
| 6 | 9 | 100 |
| 7 | 11 | 45 |
| 8 | 12 | 95 |
| 9 | 12 | 130 |
| 10 | 13 | 75 |
| 11 | 13 | 80 |
| 12 | 14 | 70 |
| 13 | 14 | 80 |
| 14 | 15 | 100 |
| 15 | 16 | 120 |
| 16 | 17 | 110 |
| 17 | 17 | 125 |
| 18 | 17 | 75 |
| 19 | 17 | 100 |
| 20 | 19 | 40 |
| 21 | 19 | 75 |
| 22 | 20 | 110 |
| 23 | 23 | 150 |
| 24 | 23 | 75 |
| 25 | 23 | 95 |
Sobre os dados acima, considere as seguintes questões:
- Todos os pacientes com fibrose cística tem o mesmo valor de PImax?
- Assumindo que a idade não afeta PImax, qual é um valor de PImax típico para pacientes com fibrose cística?
- Quão grande é a variabilidade em torno deste valor típico?
- Será que a suposição de que idade não afeta PImax é consistente com os dados?
- Se idade na verdade afeta PImax, como você descreveria o valor típico de PImax e variabilidade?
- Que tipo de representação gráfica poderia ser utilizada para visualizar adequadamente estes dados?
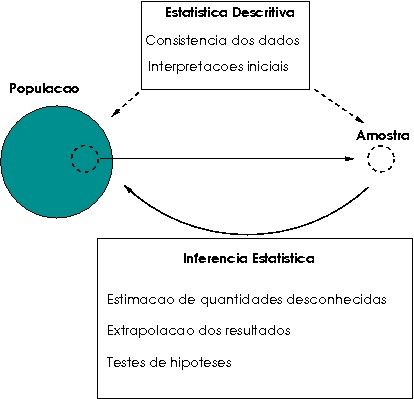
A grosso modo podemos dividir a Estatística em três áreas:
- Estatística descritiva: conjunto de técnicas destinadas a descrever e resumir dados. Reis & Reis (2001)
- Probabilidade: teoria matemática utilizada para se estudar a incerteza oriunda de fenômenos de caráter aleatório.
- Inferência estatística: técnicas que possibilitam a extrapolação, a um grande conjunto de dados (população), dos resultados obtidos a partir de um subconjunto de valores (amostra). Note que se tivermos acesso a todos os elementos que desejamos estudar, não é necessário o uso de técnicas de inferência estatística.
Estudos complexos que envolvem o tratamento estatístico dos dados, usualmente, incluem as três áreas acima.
População x amostra
Na terminologia estatística, o grande conjunto de dados que contém a característica que temos interesse recebe o nome de população. Esse termo refere-se não somente a uma coleção de indivíduos, mas também ao alvo sobre o qual reside nosso interesse (por ex: lâmpadas produzidas por uma fábrica num certo período de tempo, ou ainda todo o sangue no corpo de uma pessoa).
Algumas vezes podemos acessar toda a população para estudarmos características de interesse, mas, em muitas situações, tal procedimento não pode ser realizado por:
- razões econômicas: uma empresa geralmente não dispõe de verba suficiente para saber o que pensam todos os consumidores de seus produtos;
- razões éticas: os experimentos de laboratório envolvem uso de seres vivos;
- razões práticas: existem casos em que é impossível acessar toda a população de interesse (ex: análise de sangue de uma pessoa, e em ensaios destrutivos);
Tendo em vista as dificuldades de várias naturezas para se observar todos os elementos da população, tomaremos alguns deles para formar um grupo a ser estudado. Este subconjunto da população, em geral com dimensão sensivelmente menor, é denominado amostra.
A seleção da amostra pode ser feita de várias maneiras, dependendo, entre outros fatores, do grau de conhecimento que temos da população, da quantidade de recursos disponíveis e assim por diante.
O objetivo é tentar fornecer um subconjunto de valores o mais parecido possível com a população que lhe dá origem.
A amostragem mais usada é a amostra casual simples, em que selecionamos ao acaso, com ou sem reposição, os itens da população que farão parte da amostra.
Se houver informações adicionais a respeito da população de interesse, podemos utilizar outros esquemas de amostragem mais sofisticados.
- Amostragem estratificada: Por exemplo, se numa cidade, tivermos mais mulheres do que homens, podemos selecionar um certo número de indivíduos entre as mulheres e outro número entre homens.
- Amostragem sistemática: Pode existir uma relação numerada dos itens da população (uma lista de referência) que nos permite selecionar os indivíduos de forma pré-determinada, por ex de 8 em 8 ou de 10 em 10.
Quanto mais complexa for a amostragem maiores cuidados deverão ser tomados nas análises estatísticas utilizadas; em contrapartida, o uso de esquemas de amostragem mais elaborados pode levar a uma diminuição no tamanho de amostra necessário para uma dada precisão.
Organização de dados
Dado um conjunto de dados, como tratar os valores numéricos ou não, a fim de se extrair informações a respeito de uma ou mais características de interesse? Fazendo uso de tabelas e gráficos.
Exemplo
Um questionário foi aplicado aos alunos do primeiro ano de uma escola fornecendo as seguintes informações:
- id: identificação do aluno
- turma: turma a que o aluno foi alocado (A ou B)
- sexo: F se feminino, M se masculino
- idade: idade em anos
- alt: altura em metros
- peso: peso em quilogramas
- filhos: número de filhos na família
- fuma: hábito de fumar, sim ou não
- toler: tolerância ao cigarro: (I) indiferente, (P) incomoda pouco, (M) incomoda muito
- exerc: horas de atividade física, por semana
- cine: número de vezes em que vai ao cinema por semana
- opcine: opinão a respeito das salas de cinema na cidade: (B) regular e boa, (M) muito boa
- tv: horas gastas assistindo tv, por semana
- optv: opinião a respeito da qualidade da programação na tv: (R) ruim, (M) média, (B) boa, (N) não sabe
Tabela 1.1: Informações de questionário estudantil - dados brutos
Note que:
- A tabela de dados brutos é composta por linhas (indivíduos ou objetos) e colunas (variáveis).
- As variáveis têm naturezas diferentes: numéricas (quantitativas) e não numéricas (qualitativas).
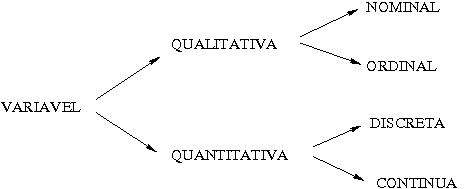
- Variáveis qualitativas podem ter: ordenação natural (qualitativa ordinal) ou não (qualitativa nominal)
- Variáveis quantitativas podem assumir: conjunto de valores é finito ou enumerável (quantitativa discreta) ou valores em intervalos dos números reais (quantitativa contínua)
Resumimos a classificação das variáveis no esquema abaixo:
Para cada tipo de variável existem técnicas apropriadas para resumir as informações, daí a vantagem de usar uma tipologia de identificação como acima.
Distribuições de freqüências
A partir da tabela de dados brutos, podemos construir a distribuição (ou tabela) de freqüências com informações resumidas para cada variável. O interesse aqui é conhecer o comportamento da variável, analisando a ocorrência de suas possíveis realizações.
Tabela 1.2: Freqüências e porcentagens dos 50 alunos pesquisados segundo a variável sexo
| Sexo | ni | fi | Porcentagem (100 fi) |
| F | 37 | 0,74 | 74 |
| M | 13 | 0,26 | 26 |
| total | n=50 | 1 | 100 |
Fonte: Tabela 1.1.
- ni: freqüência absoluta de cada classe
- n: freqüência total
- fi=ni/n: freqüência relativa ou proporção
As proporções (ou percentuais) são úteis quando se quer comparar grupos de tamanhos diferentes ou resultados de pesquisas distintas.
Por exemplo, suponhamos que se queira comparar a variável sexo para os 50 alunos daquela turma com a mesma variável para todos os alunos da escola X. Digamos que a escola tenha 2000 alunos e que a distribuição de freqüências seja a da Tabela 1.2.1.
Tabela 1.2.1: Freqüências e porcentagens dos 2000 alunos matriculados na escola X segundo a variável sexo
| Sexo | ni | fi | Porcentagem (100 fi) |
| F | 1020 | 0,51 | 51 |
| M | 880 | 0,49 | 49 |
| total | n=2000 | 1 | 100 |
Fonte: Dados hipotéticos
Não podemos comparar diretamente as colunas das freqüências das Tabelas 1.2 e 1.2.1, pois os totais de alunos são diferentes nos dois casos. Mas as colunas das proporções (porcentagens) são comparáveis, pois reduzimos as freqüências a um mesmo total.
Para variáveis cujos valores possuem ordenação natural faz sentido incluirmos também uma coluna contendo freqüências acumuladas fac. Sua utilidade principal é ajudar a estabelecer pontos de corte com uma determinada freqüência de valores da variável.
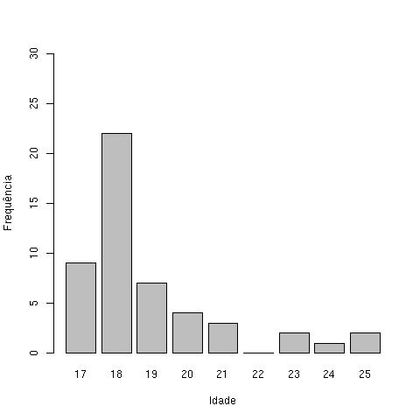
Tabela 1.3: Tabela de frequências para a variável Idade
| Idade | ni | fi | fac |
| 17 | 9 | 0,18 | 0,18 |
| 18 | 22 | 0,44 | 0,62 |
| 19 | 7 | 0,14 | 0,76 |
| 20 | 4 | 0,08 | 0,84 |
| 21 | 3 | 0,06 | 0,90 |
| 22 | 0 | 0 | 0,90 |
| 23 | 2 | 0,04 | 0,94 |
| 24 | 1 | 0,02 | 0,96 |
| 25 | 2 | 0,04 | 1,00 |
| total | n=50 | 1 |
Observe que 90% dos alunos têm idades até 21 anos, de fato até 22, uma vez que este valor tem freqüência zero.
Com relação à variável Peso (classificada como quantitativa contínua) podemos construir classes ou faixas de valores e contar o número de ocorrências em cada faixa (aqui usamos faixas de amplitude 10).
Tabela 1.4: Tabela de freqüências para a variável Peso
| Peso | ni | fi | fac |
| 40,0 ¦− 50,0 | 8 | 0,16 | 0,16 |
| 50,0 ¦− 60,0 | 22 | 0,44 | 0,60 |
| 60,0 ¦− 70,0 | 8 | 0,16 | 0,76 |
| 70,0 ¦− 80,0 | 6 | 0,12 | 0,88 |
| 80,0 ¦− 90,0 | 5 | 0,10 | 0,98 |
| 90,0 ¦− 100,0 | 1 | 0,02 | 1,00 |
| total | 50 | 1 |
Note que:
- Escolhemos incluir o extremo inferior e excluir o superior. Ex: a faixa 40,0 ¦− 50,0 não inclui os alunos com peso igual a 50,0 kg. Podemos também usar a notação [a,b) para designar o mesmo intervalo a¦− b.
- Não adotamos nenhuma regra formal quanto ao número de faixas mas utilizamos em geral, de 5 a 15 classes com a mesma amplitude. A familiaridade do pesquisador com os dados é que lhe indicará quantas e quais classes devem ser usadas. Entretanto, deve-se observar que, com um número pequeno de classes, perde-se informação, e com um número grande de classes, o objetivo de resumir os dados fica prejudicado.
- Procedendo-se desse modo, ao resumir os dados referentes a uma variável contínua, perde-se alguma informação. Por exemplo, não sabemos quais são os oito pesos da classe de 60 a 70, a não ser que investiguemos a tabela original (Tabela 1.1). Sem perda de muita precisão, poderíamos supor que todos os oito pesos fossem iguais ao ponto médio da referida classe, isto é, 65 (podemos verificar qual o erro cometido, comparado-o com os dados originais).
Quando a variável é discreta, mas com conjunto de valores muito grande (ex. variável TV) o caminho adequado é tratar a variável como se fosse contínua e criar faixas para representar seus valores.
Tabela 1.5: Tabela de frequências para a variável TV
| TV | ni | fi | fac |
| 0 ¦− 6 | 14 | 0,28 | 0,28 |
| 6 ¦− 12 | 17 | 0,34 | 0,62 |
| 12 ¦− 18 | 11 | 0,22 | 0,84 |
| 18 ¦− 24 | 4 | 0,08 | 0,92 |
| 24 ¦−¦ 36 | 4 | 0,08 | 1,00 |
| total | 50 | 1 |
Gráficos
Muitas vezes as informações contidas em tabelas podem ser mais facilmente entendidas se visualizadas através de gráficos. Graças à proliferação recursos gráficos, existe hoje uma infinidade de tipos de gráficos que podem ser utilizados (veja Figura 1.3, pág 12).
Note no entanto que a utilização de recursos visuais deve ser feita cuidadosamente; um gráfico desproporcional em suas medidas pode dar falsa impressão de desempenho e conduzir a conclusões equivocadas (Reis & Reis (2001), exemplo da pág 23).
Vamos definir três tipos básicos de gráficos: setores ou pizza, barras e histograma.
Gráfico de setores
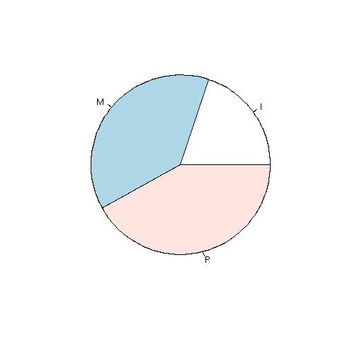
Adequado para representar variáveis qualitativas. Consiste em repartir um disco em setores circulares correspondentes às porcentagens de cada valor.
A Figura 1.4 abaixo apresenta o diagrama de disco para a variável Toler, obtida a partir da Tabela 1.1.
Gráfico de barras
Mais adequado para variáveis discretas ou qualitativas ordinais. Utiliza o plano cartesiano com os valores da variável no eixo das abscissas e as freqüências no eixo das ordenadas. Para cada valor da variável desenha-se uma barra com altura correspondendo à sua frequência.
Histograma
Consiste em retângulos contíguos com base nas faixas de valores da variável e com área igual à freqüência relativa da faixa. A altura de cada retângulo é denominada densidade de frequência ou simplesmente densidade definida pelo quociente da frequência relativa pela amplitude da faixa.
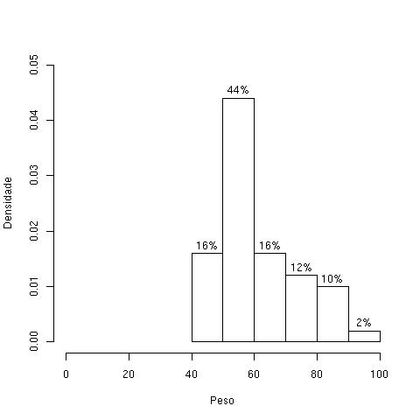
Para a variável Peso, as densidades de cada faixa podem ser obtidas dividindo-se a a coluna fi da Tabela 1.4 por 10, que é a amplitude de cada faixa. Veja o histograma obtido na Figura 1.6.
Nota: Alguns autores usam a freqüência absoluta ou porcentagem na construção do histograma. O uso da densidade impede que o histograma fique distorcido quando as faixas têm amplitudes diferentes.
Quartis
O histograma também pode ser utilizado no cálculo da mediana (mdobs), que é o valor da variável que divide o conjunto de dados ordenados em dois subgrupos de mesmo tamanho. Isto é, das observações ordenadas, 50% estão abaixo e 50% estão acima da mediana.
Exemplo 1.1: Vamos calcular a mediana da variável Peso através do histograma.
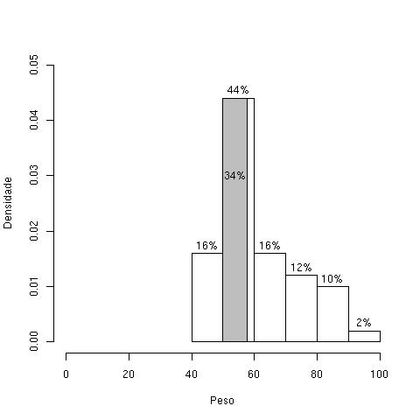
- Inicialmente identificamos o retângulo que deve conter a mediana. Como até o valor 60,0 kg temos acumuladas 60% das observações conluímos que a mediana pertence ao intervalo [50,0; 60,0).
- Dentro da faixa [50,0; 60,0) precisamos determinar um retângulo com percentual igual a 34%, que é o que falta para atingir os 50%.
- Com uso de proporções, estabelecemos a seguinte igualdade:
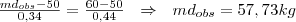
O conceito de mediana pode ser generalizado para situações em que o conjunto de dados é dividido em mais do que dois subgrupos. No caso de 4 subgrupos, além da mediana, dois valores tais que 25% das observações ordenadas estarão abaixo de um deles (primeiro quartil (Q1)) e 75% estarão abaixo do outro (terceiro quartil (Q3)).
Note que a mediana representa o segundo quartil (Q2).
O cálculo dos valores dos quartis também pode ser feito através do histograma.
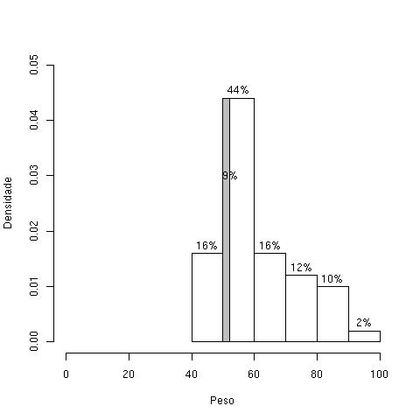
Exemplo 1.2: No histograma da variável Peso, vemos que o valor de Q1 se encontra no intervalo [50,0; 60,0), ie corresponderá ao valor Q1 que determinará um percentual de 9% no retângulo correspondente:
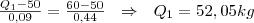
O terceiro quartil pode ser obtido de forma semelhante (Q3=69,38).
Para o cálculo de quartis usando a tabela de dados brutos, precisamos ordenar as observações e escolher os valores que dividem os dados nas proporções desejadas. Em alguns casos pode ser necessário tomar médias de valores vizinhos.
Box-Plot
É uma forma de representação gráfica dos quartis.
- Definimos uma "caixa" com o nível superior dado por Q3 e o nível inferior por Q1.
- A mediana é representada por um traço no interior da caixa
- Segmentos de reta são colocados da caixa até os valores máximo e mínimo, desde que estas não sejam observações discrepantes1).
Exemplo 1.3: Suponha que um produtor de laranjas costuma guardar as frutas em caixas e está interessado em estudar o número de laranjas por caixa. Após um dia de colheita, 20 caixas foram contadas. Os resultados brutos, após a ordenação, são:
22 29 33 35 35 37 38 43 43 44 48 48 52 53 55 57 61 62 67 69
Para estes dados temos que:
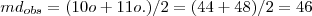
- Q1=36 e Q3=56
- Min=22
- Máx=69
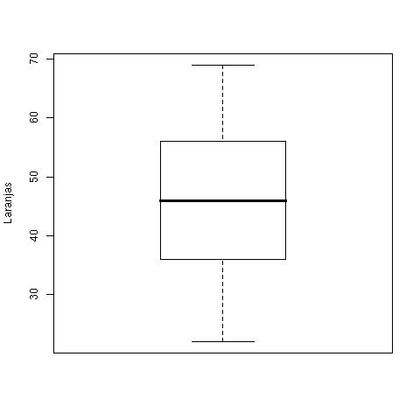
O box-plot correspondente é apresentado na Figura 1.7.
A representação gráfica através do box-plot informa, dentre outras coisas, a variabilidade e simetria dos dados. Na Figura 1.7 os dados apresentam simetria acentuada2).
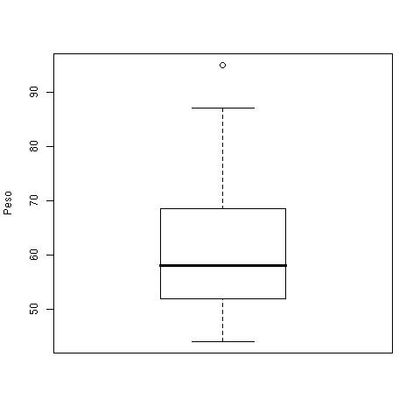
O box-plot para a variável Peso (Figura 1.8) por outro lado, apresenta uma pequena assimetria.
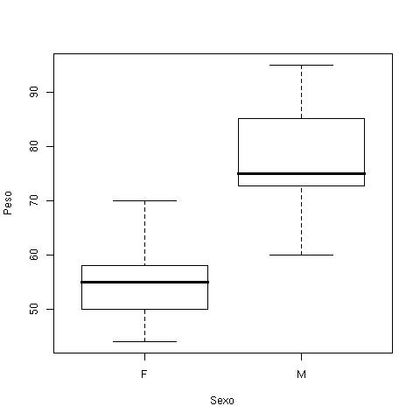
Gráficos do tipo box-plot também são úteis para detectar, descritivamente, diferenças nos comportamentos de grupos de variáveis (veja exemplo na Figura 1.9).
Podemos notar que os homens apresentam peso mediano superior ao das mulheres, além de uma maior variablidade e mais assimetria nos dados.
Exercício
Um pesquisador está interessado em fazer um levantamento sobre alguns aspectos sócioeconômicos dos empregados da seção de orçamentos da Companhia MB. Usando informações obtidas do departamento pessoal, ele elaborou a Tabela 1.
Tabela 1: CONJUNTO DE DADOS MILSA