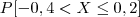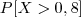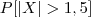Verificar sua familiaridade com o R executando as seguintes tarefas:
| Indivíduo | Idade | Time |
| 1 | 23 | Coxa |
| 2 | 31 | Coxa |
| 3 | 24 | Coxa |
| 4 | 19 | Furacão |
| 5 | 33 | Furacão |
| 6 | 32 | Furacao |
| 7 | 30 | Coxa |
| 8 | 35 | Furacao |
| 9 | 22 | Coxa |
| 10 | 21 | Furacao |
Conteúdo de óleo de S. linicola, em percentagem, em vários estágios de crescimento (Steel & Torrie, 1980, p.199).
| Estágios | Blocos |
| | I | II | III | IV |
| Estágio 1 | 4,4 | 5,9 | 6,0 | 4,1 |
| Estágio 2 | 3,3 | 1,9 | 4,9 | 7,1 |
| Estágio 3 | 4,4 | 4,0 | 4,5 | 3,1 |
| Estágio 4 | 6,8 | 6,6 | 7,0 | 6,4 |
| Estágio 5 | 6,3 | 4,9 | 5,9 | 7,1 |
| Estágio 6 | 6,4 | 7,3 | 7,7 | 6,7 |
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| y | 0.9 | 5.1 | 2.4 | 8.1 | 4.2 | 7.1 | 5.6 | 7.6 | 5.9 | 7.7 | 11.8 | 6.9 | 9.3 | 10.9 | 8.4 | 11.6 | 13.0 | 13.8 | 13.1 | 9.3 |
Considere as observações a seguir
9 5 2 3 0 3 2 4 14 3 4 1 0 6 1
Assumindo a distribuição Geométrica:
fazer um gráfico da função de (log)-verossimilhança das observações a seguir, assumindo a distribuição Geométrica
encontrar o ponto de máximo da função utilizando um procedimento numérico
Considere dados de um normal de média
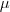
e variância 16. Traçar a função de verossimilhança e encontrar a estimativa em cada uma das seguintes situações:
se os dados forem:
23 24 27 20 32 26 28
se além dos dados acima sabemos que temos dois outros dados acima de 30
e se soubermos que temos mais três dados entre 28 e 30
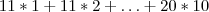
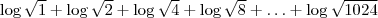 , em que
, em que 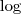 é o logarítmo neperiano.
é o logarítmo neperiano.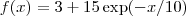
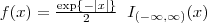 . Mostre comandos para obter:
. Mostre comandos para obter: 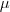 e variância 16. Traçar a função de verossimilhança e encontrar a estimativa em cada uma das seguintes situações:
e variância 16. Traçar a função de verossimilhança e encontrar a estimativa em cada uma das seguintes situações: