A joint model proposal????

1. Arquivo Sweave com o modelo proposto

Ao olhar as simulacoes e a descrio de como eram feitas que vc me fez eu sempre achei muito complicado de explicar de forma breve e facil de entender. Resolvi entao pensar em uma outra forma mais direta de ferar simulacoes relacionando as proporcoes com a abundancia.

Tive entao a ideia de fazer segundo um modelo onde poderiamos controlar por parametros o que desejamos. Veja o seguinte e me diga o que acha:

1. Simular Y que representa a abundancia total

Daqui para frente seguem duas sequencias de possiveis procedimentos:

A. proporções como funções perfeitas de Y

A.2. Obter
      p1 <- exp(1*Y)/(1+exp(1*Y))
A.3  Obter
      p2 <- exp(0.5*Y)/(1+0.5*Y)
A.4  Obter
      p3 <- 2 - p1 - p2
A.5  Transformar p1, p2 e p3 em composicoes dovidindo cada um pela soma
     de todos eles

Neste caso note que p1 mais relacionado com Y, p2 menos varivel e p3 tem uma correlacao negativa com estes.

Poderia-se ainda somar (subtrair uma constante para forcar proporcoes mais altas ou baixas)

Para intuicao sobre os valores veja:

 y <- grf(100, cov.pars=c(1, .25))$data
 p1 <- exp(y)/(1+exp(y))
 range(p1)
[1] 0.1567524 0.8486654
 p2 <- exp(0.5*y)/(1+exp(0.5*y))
 range(p2)
[1] 0.3012618 0.7030963
 p2 <- exp(1+0.5*y)/(1+exp(1+0.5*y))
 range(p2)
[1] 0.5395928 0.8655399
 range(p1+p2)
[1] 0.6963451 1.7142053
 p3 <- 2 - p1 - p2
 pt <- p1+p2+p3
 p1 <- p1/pt; p2 <- p2/pt; p3 <- p3/pt
 plot(cbind(p1,p2,p3))

A de forrma geral transformacao e' dada por

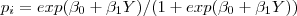
e os valores d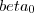e e 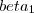controlam o comportamento e com isto poderia-se escolher qual a calsse a ser representada por cada um deles.

B. Semelhante a anterior porem adicionando uma aleatoriedade nas proporcoes B.2. Obter como anterior porem adicionando um "ruido", trocando Y no algoritmo anterior por

Y + rnorm(length(y), m=0, sd=0.1)

Depois fazer o mesmo para p2 e o resto fica como no algortmo anterior

E….. acho que acabo de inventar um novo modelo para modelagem conjunta!!!!!

Comentário adicional: para fechar o modelo seria bom que os p's já fosse gerados de forma a somar 1 sem a necessidade de "padronizar". Imagino que deve ser possível impor uma restrição nos coeficientes 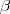para garantir isto.
Uma outra possibilidade é dividir as probs p1 e p2 por 2 e com isto garantir qq beta ser válido – ver os efeitos disto pois coloca um limite de 0.5 em p1 e p2 o que pode nao ser uma boa ideia…

Em uma ou outra situação ainda nao está claro como gerar uma situação onde uma das classes possa ter quase 100% – talvez pensar em algo como multiplicar as proporcoes ou na escala LRT

pensando melhor… pensando melhor no que escrevi antes acho que me empolguei meio rápido demais:

1. p3 precisa ser calculado associado aos betas tb caso contrário se for feito por diferenca como propus inicialmente composicoes (p1 e p2) que ficam restritas a serem menores que 0.5. Com isto acho que o modelo válido
2. me parece ainda que uma outra idéia para gerar associação estava bem na nossa frente e nao percebemos: usar o modelo multinomial com a abundância como covárivel!!! - no paper isto pode ter certa vantagem por unificar com o diagnóstico que utilizamos. Seria bom fazer umas simu;ação [para ver as situações geradas.

require(lattice)
require(MASS)
require(geoR)
 
gs <- expand.grid((0:10)/10, (0:10)/10)
 
# basic gaussians to be used posteriorly 
s2 <- 0.5
Sig <- diag(c(1,1,1,1,1))
Sig[1,4] <- 0.9
Sig[4,1] <- 0.9
Sig <- Sig*s2
Sig
m0 <- mvrnorm(nrow(gs), c(2,0,0,0,0), Sig)
plot(as.data.frame(m0))
cor(m0)
 
# Generate a spatial Gaussian process Y
phi <- 0.25
sigmasq <- 1
Y <- grf(grid=gs, cov.pars=c(sigmasq, phi))
Y$data <- exp(m0[,1]+Y$data)
var(log(Y$data))
 
## option 1: age compositions independent from Y
# Generate age compositions independent from Y
comp.1 <- t(apply(cbind(exp(m0[,c(2,3)]),1),1,function(x) x/sum(x)))
dim(comp.1)
apply(comp.1, 2, range)
cor(cbind(comp.1, log(Y$data)))
plot(as.data.frame(cbind(comp.1, log(Y$data))))
 
lr.1 <- data.frame(lr13 = log(comp.1[,1]/comp.1[,3]), lr23 = log(comp.1[,2]/comp.1[,3]), Y=log(Y$data))
cor(lr.1)
cor(lr.1, met="spea")
plot(lr.1)
 
 
# Build abundance at age 
Yi.1 <- comp.1*Y$data 
dim(Yi.1)
cor(cbind(Yi.1, log(Y$data)))
plot(as.data.frame(cbind(Yi.1, log(Y$data))))
 
## option 2: age compositions dependent from Y
# Generate age compositions dependent from Y
comp.2 <- t(apply(cbind(exp(m0[,c(3,4)]),1),1,function(x) x/sum(x)))
apply(comp.1, 2, range)
cor(cbind(comp.2, log(Y$data)))
cor(cbind(comp.2, log(Y$data)), met="spea")
plot(as.data.frame(cbind(comp.2, log(Y$data))))
 
lr.2 <- data.frame(lr13 = log(comp.2[,1]/comp.2[,3]), lr23 = log(comp.2[,2]/comp.2[,3]), Y=log(Y$data))
cor(lr.2)
cor(lr.2, met="spea")
plot(lr.2)
 
lr.2a <- data.frame(lr12 = log(comp.2[,1]/comp.2[,2]), lr32 = log(comp.2[,3]/comp.2[,2]), Y=log(Y$data))
cor(lr.2a)
cor(lr.2a, met="spea")
plot(lr.2a)
 
# Build abundance at age 
Yi.2 <- comp.2*Y$data 
dim(Yi.2)
cor(cbind(Yi.2, log(Y$data)))
plot(as.data.frame(cbind(Yi.2, log(Y$data))))
 
df0 <- data.frame(abund=c(Yi.1,Yi.2), comp=c(comp.1,comp.2),Y=Y$data, opt=rep(c("indep","dep"),
                  rep(length(comp.1),2)), age=rep(rep(c(1,2,3),2),rep(length(comp.1)/3,6)))
 
# plots
xyplot(comp~log(Y)|age*opt,data=df0)
xyplot(abund~Y|age*opt,data=df0)
plot(as.geodata(Y))

O problema que temos nestes casos em que simulamos Y e depois obtemos Yi por Y*pi é que a estrutura espacial dos Yi vai ser exactamente a mesma. Se acrescentarmos variabilidade com estrutura espacial temos que recalcular os pi …

PJ: De fato mas para fazer diferente teria que simular de outra forma pois aqui só tem um Y geoestatistico gerado. O modelo multivariado conjunto para os LR seria a alternativa. Por outro lado eu nao vejo muito problema nesta fato pois as correlacoes entra as composicoes de certa forma tratam isto.